题目内容
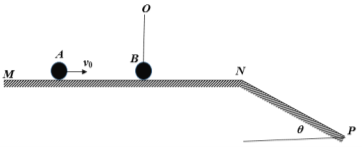
【题目】如图所示，在磁感应强度为B，方向垂直纸面向里的匀强磁场中有一粒子源，离子源从O点在纸面内均匀地向各个方向同时发射速率为v、比荷为k的带正电的粒子，PQ是在纸面内垂直磁场放置的厚度不计的挡板，挡板的P端与O点的连线与挡板垂直，距离为
，且粒子打在挡板上会被吸收；不计带电粒子的重力与粒子间的相互作用，磁场分布足够大，求：
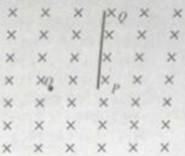
（1）为使最多的粒子打在板上，则挡板至少多长；
（2）若挡板足够长，则打在板上的粒子在磁场中运动的最长时间与最短时间的差值是多少；
（3）若挡板足够长，在打在挡板上的粒子占所有粒子的比率是多少.
【答案】（1）
（2）
（3）
【解析】（1）设带电粒子的质量为m，带电量为q，粒子在磁场中受到洛伦兹力提供做圆周运动的向心力，设粒子做圆周运动的半径为r，则有
解得： 
在挡板左侧能打在挡板上部最远点的粒子恰好与挡板相切，如图所示，由题意
，由几何知识可得： 
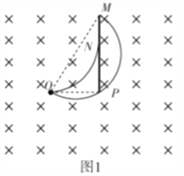
设粒子初速度方向与OP夹角为θ，随着θ从0开始逐渐增大，粒子打在挡板上的点从N点逐渐下移；当粒子刚好通过P点时，粒子开始打在挡板的右侧，设此时打在挡板上的点为M，如图1所示，在OPM中，由几何关系可得： 
所以
；
当夹角θ继续增大，则粒子打在挡板上的点从M点逐渐下移至P点，由以上分析知道，挡板长度至少等于
时，挡板吸收的粒子数最多；
（2）由以上分析知，当粒子恰好从左侧打在P点时，时间最短，如图2轨迹1所示，由几何知识得粒子转过的圆心角为
；当粒子从右侧恰好打在P点时，时间最长，如轨迹2所示，由几何知识得粒子转过的圆心角为
粒子的运动周期
沿轨迹1的时间
沿轨迹2的时间
最长的时间差
（3）粒子出射方向水平向右的粒子和沿轨迹2的粒子速度方向之间都能打在板上粒子方向的夹角为
打到板上的粒子占所有粒子的比率为： 
解得： 
名校课堂系列答案
