题目内容
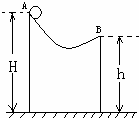 如图所示,光滑曲面的两端A、B离地面的高度分别为H和h,一小球自A端由静止释放沿曲面下滑并经过B端飞出落地,则小球经过B端时的速率与刚落地时的速率之比为( )
如图所示,光滑曲面的两端A、B离地面的高度分别为H和h,一小球自A端由静止释放沿曲面下滑并经过B端飞出落地,则小球经过B端时的速率与刚落地时的速率之比为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:小球运动的过程中,只有重力做功,机械能守恒,根据机械能守恒定律求解即可.
解答:解:小球运动的过程中,只有重力做功,机械能守恒,则得:
从A到B过程,有:mgH=mgh+
m
,得 vB=
从A到地过程,有:mgH=
m
,得 v地=
所以有:
=
故选:C
从A到B过程,有:mgH=mgh+
| 1 |
| 2 |
| v | 2 B |
| 2g(H-h) |
从A到地过程,有:mgH=
| 1 |
| 2 |
| v | 2 地 |
| 2gH |
所以有:
| vB |
| v地 |
|
故选:C
点评:对于没有摩擦的情形,往往优先考虑机械能是否守恒.运用机械能守恒定律时,可根据重力势能变化量与动能变化量大小相等列式,可不必选取参考平面.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
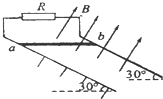 光滑的平行金属导轨长L=2m,两导轨间距d=0.5m,轨道平面与水平面的夹角 θ=30°,导轨上端接一阻值为R=0.6Ω的电阻,轨道所在空间有垂直轨道平面向上的匀强磁场,磁场的磁感应强度B=1T,如图所示.有一质量m=0.5kg、电阻r=0.4Ω的金属棒曲,放在导轨最上端,其余部分点阻不计.当棒ab从轨道最上端由静止开始下滑到底端脱离轨道时,电阻R上产生的热量Q1=0.6J,取g=10m/s2,试求:
光滑的平行金属导轨长L=2m,两导轨间距d=0.5m,轨道平面与水平面的夹角 θ=30°,导轨上端接一阻值为R=0.6Ω的电阻,轨道所在空间有垂直轨道平面向上的匀强磁场,磁场的磁感应强度B=1T,如图所示.有一质量m=0.5kg、电阻r=0.4Ω的金属棒曲,放在导轨最上端,其余部分点阻不计.当棒ab从轨道最上端由静止开始下滑到底端脱离轨道时,电阻R上产生的热量Q1=0.6J,取g=10m/s2,试求:
