题目内容
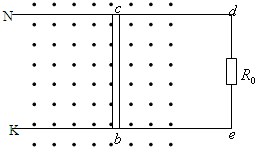
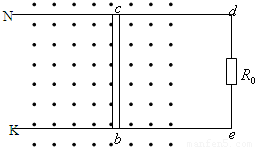
如图,在一水平面内有两根平行的金属导轨Nd、Ke,其电阻不计,导轨上有一根金属棒bc,长L=0.5m,质量m=0.1kg,与导轨接触良好,可在导轨上无摩擦地滑动,bc的电阻R=0.2Ω.竖直向上的匀强磁场磁感应强度B=0.1T,导轨的右端接有电阻R=0.3Ω,导轨左端足够长.(1)给棒bc外加一个水平向左的拉力,使其从静止开始向左作加速度为a=4m/s2的匀变速直线运动,运动到5s末时,这个拉力为多大?
(2)若把拉力刚作用于静止的bc棒的时刻取为计时的0时刻,拉力大小变化规律为F=(2.5×10-2t+0.5)N,式中t的单位是秒,拉力的方向水平向左,经过一段时间,力F对bc棒做功54J,试论证在这段时间内电阻R上的发热量小于32.4J.
(3)在第(2)问的条件下,bc棒的加速度只能是以下两种情况中一种.请你判断哪种情况是正确的,并按相应要求作答:(不要求写出作判断的推理过程)
(Ⅰ)bc的加速度恒定(请求出这个加速度的大小)
(Ⅱ)bc的加速度变化(请定性地指出这个加速度的增减情况)
【答案】分析:(1)根据匀变速直线运动的速度时间公式求出5s末的速度,结合E=BLv、闭合电路欧姆定律和牛顿第二定律求出拉力的大小.
(2)根据动能定理得出外力做功与整个回路产生热量与动能增量的关系,通过闭合电路欧姆定律得出电阻R上的发热量与整个回路产生热量的关系,根据以上规律进行求解,得出电阻R上的发热量的范围.
(3)根据牛顿第二定律得出拉力F的表达式,与拉力的变化规律的表达式进行比较,确定bc的加速度变化.根据表达式得出加速度的大小.
解答:解:(1)v=at=20m/s
F-F安=ma
则
代入数据解得F=0.5N.
(2)证明:根据动能定理
WF-Q总=△EK
因为

解得
则54-
QR0<32.4J.
(3)(Ⅰ)正确
v=at
F-F安=ma
则
F=0.005at+0.1a
F=2.5×10-2t+0.5 则0.1a=0.5
解得a=5m/s2.
答:(1)拉力为0.5N.
(2)证明如上.
(3)(Ⅰ)正确,加速度的大小为5m/s2.
点评:本题综合考查了牛顿第二定律、动能定理以及切割产生的感应电动势公式和闭合电路欧姆定律,综合性较强,难度不大,是一道好题.
(2)根据动能定理得出外力做功与整个回路产生热量与动能增量的关系,通过闭合电路欧姆定律得出电阻R上的发热量与整个回路产生热量的关系,根据以上规律进行求解,得出电阻R上的发热量的范围.
(3)根据牛顿第二定律得出拉力F的表达式,与拉力的变化规律的表达式进行比较,确定bc的加速度变化.根据表达式得出加速度的大小.
解答:解:(1)v=at=20m/s
F-F安=ma
则

代入数据解得F=0.5N.
(2)证明:根据动能定理
WF-Q总=△EK
因为


解得

则54-

QR0<32.4J.
(3)(Ⅰ)正确
v=at
F-F安=ma
则

F=0.005at+0.1a
F=2.5×10-2t+0.5 则0.1a=0.5
解得a=5m/s2.
答:(1)拉力为0.5N.
(2)证明如上.
(3)(Ⅰ)正确,加速度的大小为5m/s2.
点评:本题综合考查了牛顿第二定律、动能定理以及切割产生的感应电动势公式和闭合电路欧姆定律,综合性较强,难度不大,是一道好题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

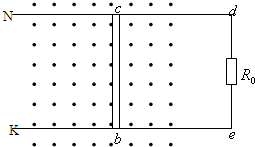 如图,在一水平面内有两根平行的金属导轨Nd、Ke,其电阻不计,导轨上有一根金属棒bc,长L=0.5m,质量m=0.1kg,与导轨接触良好,可在导轨上无摩擦地滑动,bc的电阻R=0.2Ω.竖直向上的匀强磁场磁感应强度B=0.1T,导轨的右端接有电阻R0=0.3Ω,导轨左端足够长.
如图,在一水平面内有两根平行的金属导轨Nd、Ke,其电阻不计,导轨上有一根金属棒bc,长L=0.5m,质量m=0.1kg,与导轨接触良好,可在导轨上无摩擦地滑动,bc的电阻R=0.2Ω.竖直向上的匀强磁场磁感应强度B=0.1T,导轨的右端接有电阻R0=0.3Ω,导轨左端足够长.