题目内容
翼型飞行器有很好的飞行性能．其原理是通过对降落伞的调节，使空气升力和空气阻力都受到影响．同时通过控制动力的大小而改变飞行器的飞行状态．已知：飞行器的动力F始终与飞行方向相同，空气升力F1与飞行方向垂直，大小与速度的平方成正比，即F1=C1v2；空气阻力F2与飞行方向相反，大小与速度的平方成正比，即F2=C2v2．其中C1、C2相互影响，可由运动员调节，满足如图1所示的关系．飞行员和装备的总质量为90kg．重力加速度取g=10m/s2．
（1）若飞行员使飞行器以v1=10
m/s速度在空中沿水平方向匀速飞行，如图2所示．则飞行器受到动力F大小为多少？
（2）若飞行员关闭飞行器的动力，使飞行器匀速滑行，且滑行速度v2与地平线的夹角θ=30°，如图3所示，则速度v2的大小为多少？（结果可用根式表示）
（3）若飞行员使飞行器在空中的某一水平面内做匀速圆周运动，如图4所示，在此过程中C2只能在1.75～2.5N?s2/m2之间调节，且C1、C2的大小与飞行器的倾斜程度无关．则飞行器绕行一周动力F做功的最小值为多少？
（1）若飞行员使飞行器以v1=10
| 3 |
（2）若飞行员关闭飞行器的动力，使飞行器匀速滑行，且滑行速度v2与地平线的夹角θ=30°，如图3所示，则速度v2的大小为多少？（结果可用根式表示）
（3）若飞行员使飞行器在空中的某一水平面内做匀速圆周运动，如图4所示，在此过程中C2只能在1.75～2.5N?s2/m2之间调节，且C1、C2的大小与飞行器的倾斜程度无关．则飞行器绕行一周动力F做功的最小值为多少？
分析：（1）物体做直线运动的条件是所受的合力方向与速度方向在一条直线上，根据运动员和翼型伞的受力情况进行判断；
（2）由①位置的受力分析，匀速运动时对重力进行分解，根据平衡条件求解；
（3）竖直方向匀速运动，水平方向做圆周运动，根据力的做功表达式，结合前面条件，即可求解．
（2）由①位置的受力分析，匀速运动时对重力进行分解，根据平衡条件求解；
（3）竖直方向匀速运动，水平方向做圆周运动，根据力的做功表达式，结合前面条件，即可求解．
解答：解：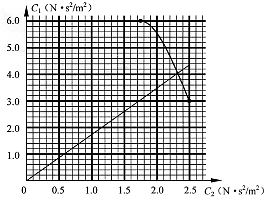
（1）由受力分析可知：mg=C1v12
得C1=3N?s2/m2
由C1、C2关系图象可得
C2=2.5N?s2/m2
动力F=F2=C2v12
所以F=750N
（2）由受力分析可知：
mgcosθ=C1v22
mgsinθ=C2v22
又C1=C2cotθ
在图1中过原点作直线正确得到直线与曲线的交点
C2=2.3N?s2/m2
C1=4N?s2/m2
得v2约为
m/s
（3）设此时飞行器飞行速率为v，圆周运动的半径为R，F1与竖直方向夹角为α，则有：
竖直方向合力为零：mg=C1v2cosα
水平方向合力提供向心力：C1v2sinα=
动力：F=F2=C2v2
绕行一周动力做的功为W=F?2πR=
当C2=1.75N?s2/m2，C1=6N?s2/m2，α=45°时，W有最小值．
Wmin=15750πJ=49455J
答：（1）则飞行器受到动力F大小为750N；
（2）则速度v2的大小为为
m/s；
（3）则飞行器绕行一周动力F做功的最小值为49455J．
（1）由受力分析可知：mg=C1v12得C1=3N?s2/m2
由C1、C2关系图象可得
C2=2.5N?s2/m2
动力F=F2=C2v12
所以F=750N
（2）由受力分析可知：
mgcosθ=C1v22
mgsinθ=C2v22
又C1=C2cotθ
在图1中过原点作直线正确得到直线与曲线的交点
C2=2.3N?s2/m2
C1=4N?s2/m2
得v2约为
| 195 |
（3）设此时飞行器飞行速率为v，圆周运动的半径为R，F1与竖直方向夹角为α，则有：
竖直方向合力为零：mg=C1v2cosα
水平方向合力提供向心力：C1v2sinα=
| mv2 |
| R |
动力：F=F2=C2v2
绕行一周动力做的功为W=F?2πR=
| 2πC2m2g | ||
|
当C2=1.75N?s2/m2，C1=6N?s2/m2，α=45°时，W有最小值．
Wmin=15750πJ=49455J
答：（1）则飞行器受到动力F大小为750N；
（2）则速度v2的大小为为
| 195 |
（3）则飞行器绕行一周动力F做功的最小值为49455J．
点评：本题有一定的难度，能正确的理解题目所提示的信息，并有一定的数据解读能力是解决该题的关键．
练习册系列答案
相关题目
速度在空中沿水平方向匀速飞行，如图2所示。则飞行器受到动力F大小为多少？
与地平线的夹角θ=30°。如图3所示。则速度翼型飞行器有很好的飞行性能．其原理是通过对降落伞的调节，使空气升力和空气阻力都受到影响．同时通过控制动力的大小而改变飞行器的飞行状态．已知：飞行器的动力F始终与飞行方向相同，空气升力F1与飞行方向垂直，大小与速度的平方成正比，即F1=C1v2；空气阻力F2与飞行方向相反，大小与速度的平方成正比，即F2=C2v2．其中C1、C2相互影响，可由运动员调节，满足如图1所示的关系．飞行员和装备的总质量为90kg．（重力加速度取g＝10m/s2．）
 |
、
（1）若飞行员使飞行器以
速度在空中沿水平方向匀速飞行，如图2所示．则飞行器受到动力F大小为多少？
（2）若飞行员关闭飞行器的动力，使飞行器匀速滑行，且滑行速度v2与地平线的夹角θ=30°，如图3所示，则速度v2的大小为多少？（结果可用根式表示）
（3）若飞行员使飞行器在空中的某一水平面内做匀速圆周运动，如图4所示，在此过程中C2只能在1.75~2.5N·s2/m2之间调节，且C1、C2的大小与飞行器的倾斜程度无关．则飞行器绕行一周动力F做功的最小值为多少？（结果可保留π．）