题目内容
17.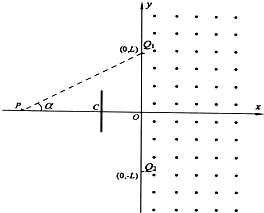 如图所示的xOy坐标系中,Y轴右侧空间存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直于xOy平面向外.Ql、Q2两点的坐标分别为(0,L)、(0,-L),坐标为(-$\frac{\sqrt{3}}{3}$L,0)处的C点固定一平行于y轴放置的绝缘弹性挡板,C为挡板中点.带电粒子与弹性绝缘挡板碰撞前后,沿y轴方向分速度不变,沿x轴方向分速度反向,大小不变.现有质量为m,电量为+q的粒子,在P点沿PQ1方向进入磁场,α=30°,不计粒子重力.
如图所示的xOy坐标系中,Y轴右侧空间存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直于xOy平面向外.Ql、Q2两点的坐标分别为(0,L)、(0,-L),坐标为(-$\frac{\sqrt{3}}{3}$L,0)处的C点固定一平行于y轴放置的绝缘弹性挡板,C为挡板中点.带电粒子与弹性绝缘挡板碰撞前后,沿y轴方向分速度不变,沿x轴方向分速度反向,大小不变.现有质量为m,电量为+q的粒子,在P点沿PQ1方向进入磁场,α=30°,不计粒子重力.(1)若粒子从点Q1直接通过点Q2,求粒子初速度大小.
(2)若粒子从点Q1直接通过点O,求粒子第一次经过x轴的交点坐标.
(3)若粒子与挡板碰撞两次并能回到P点,求粒子初速度大小及挡板的最小长度.
分析 (1)作出粒子运动的轨迹图,结合几何关系求出粒子在磁场中运动的轨道半径,根据半径公式求出粒子的速度.
(2)作出粒子运动的轨迹图,根据几何关系求出粒子运动的半径,通过几何关系求出第一次经过x轴的交点坐标;
(3)抓住与挡板碰撞两次并能回到P点,作出轨迹图,结合几何关系,运用半径公式进行求解.
解答 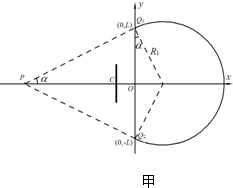 解:(1)由题意画出粒子运动轨迹如图甲所示,粒子在磁场中做圆周运动的半径大小为R1,由几何关系得R1cos30°=L…(1)
解:(1)由题意画出粒子运动轨迹如图甲所示,粒子在磁场中做圆周运动的半径大小为R1,由几何关系得R1cos30°=L…(1)
粒子磁场中做匀速圆周运动,有:$qvB=m\frac{{{v_1}^2}}{R_1}$…(2)
解得:${v_1}=\frac{{2\sqrt{3}qBL}}{3m}$…(3)
(2)由题意画出粒子运动轨迹如图乙所示,设其与x轴交点为M,横坐标为xM,由几何关系知:2R2cos30°=L…(4)
xM=2R2sin30°…(5)
则M点坐标为($\frac{{\sqrt{3}}}{3}L,0$)…(6)
(3)由题意画出粒子运动轨迹如图丙所示,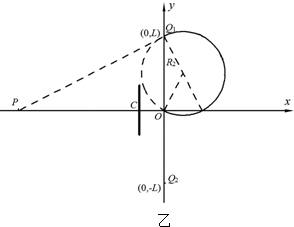 粒子在磁场中做圆周运动的半径大小为R3,
粒子在磁场中做圆周运动的半径大小为R3,
偏转一次后在y负方向偏移量为△y1,由几何关系得:△y1=2R3cos30°…(7)
为保证粒子最终能回到P,粒子每次射出磁场时速度方向与PQ2连线平行,与挡板碰撞后,速度方向应与PQ1连线平行,每碰撞一次,粒子出进磁场在y轴上距离△y2(如图中A、E间距)可由题给条件得:
$△{y}_{2}=\frac{2\sqrt{3}L}{3}tan30°$…(8)
当粒子只碰二次,其几何条件是:3△y1-2△y2=2L…(9)
解得:${R}_{3}=\frac{10\sqrt{3}L}{27}$…(10)
粒子磁场中做匀速圆周运动,有:$q{v}_{3}B=m\frac{{{v}_{3}}^{2}}{{R}_{3}}$…(11)
解得:${v_3}=\frac{{10\sqrt{3}qBL}}{27m}$…(12)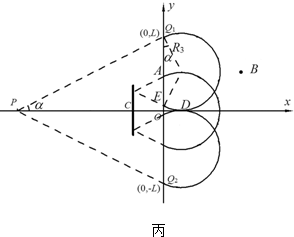 挡板的最小长度为:$△L=2{R_3}cos{30°}-\frac{{2\sqrt{3}L}}{3}tan{30°}$…(13)
挡板的最小长度为:$△L=2{R_3}cos{30°}-\frac{{2\sqrt{3}L}}{3}tan{30°}$…(13)
解得:$△L=\frac{4L}{9}$…(14)
答:(1)粒子初速度大小为$\frac{2\sqrt{3}qBL}{3m}$;
(2)粒子第一次经过x轴的交点坐标为($\frac{{\sqrt{3}}}{3}L,0$)
(3)粒子初速度大小为$\frac{10\sqrt{3}qBL}{27m}$,挡板的最小长度为$\frac{4L}{9}$.
点评 本题考查了粒子在磁场中的运动,对于三小问,关键作出三种粒子的轨迹图,结合几何关系,运用半径公式进行求解,难度较大,对数学几何的关系要求较高,需加强这方面的训练.

| A. | 库仑在研究电荷间相互作用时,提出了“电场”的概念 | |
| B. | 无论是亚里士多德、伽利略,还是笛卡尔都没有建立力的概念,而牛顿的伟大之处在于他将物体间复杂多样的相互作用抽象为“力”,为提出牛顿第一定律而确立了一个重要的物理概念 | |
| C. | 卡文迪许通过扭秤实验测出了静电力常量 | |
| D. | 欧姆定律I=$\frac{U}{R}$采用比值定义法定义了电流强度这一物理量 |
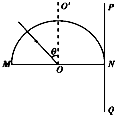 固定的半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线,足够大的
固定的半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线,足够大的光屏PQ紧靠玻璃砖右侧且垂直于MN,由A、B两种单色光组成的一束光沿半径方向射向O点,入射光线与OO′夹角θ较小时,光屏NQ区域出现两个光斑,逐渐增大θ角.当θ=α时,光屏NQ区城A光的光斑消失,继续增大θ角,当θ=β时,光屏NQ区域B光的光斑消失,则下列说法中正确的是( )
| A. | A光在MN面发生全反射的临界角比B光的在MN面发生全反射的临界角大 | |
| B. | 玻璃砖对A光的折射率比对B光的大 | |
| C. | A光在玻璃砖中传播速度比B光的大 | |
| D. | α<θ<β时,光屏PQ上有2个光斑 | |
| E. | β<θ<$\frac{π}{2}$时,光屏PQ上只有1个光斑 |
 如图所示为a、b两小球沿光滑水平面相向运动的v-t图.已知当两小球间距小于或等于L时,受到相互排斥的恒力作用,当间距大于L时,相互间作用力为零.由图可知( )
如图所示为a、b两小球沿光滑水平面相向运动的v-t图.已知当两小球间距小于或等于L时,受到相互排斥的恒力作用,当间距大于L时,相互间作用力为零.由图可知( )| A. | a球的质量大于b球的质量 | B. | a球的质量小于b球的质量 | ||
| C. | t1时刻两球间距最小 | D. | t3时刻两球间距为L |
| A. | 1 kg铜所含的原子数为$\frac{{N}_{A}}{M}$ | B. | 1 m3铜所含的原子数为$\frac{M{N}_{A}}{ρ}$ | ||
| C. | 1个铜原子的质量为$\frac{M}{{N}_{A}}$(kg) | D. | 1个铜原子的体积为$\frac{M}{ρ{N}_{A}}$(m3) |
| A. | 振子正在做加速运动,加速度正在增加 | |
| B. | 振子正在做加速运动,加速度正在减少 | |
| C. | 振子正在做减速运动,加速度正在增加 | |
| D. | 振子正在做减速运动,加速度正在减少 |
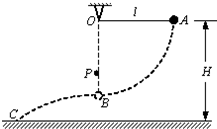 一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.求:
一长l=0.80m的轻绳一端固定在O点,另一端连接一质量m=0.10kg的小球,悬点O距离水平地面的高度H=1.00m.开始时小球处于A点,此时轻绳拉直处于水平方向上,如图所示.让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的钉子P时立刻断裂.不计轻绳断裂的能量损失,取重力加速度g=10m/s2.求: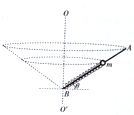 如图所示,光滑杆AB长为L,其B端固定一根劲度系数为k=100N/m,原长为l0=0.4m的轻质弹簧,质量为m=1kg的小球套在光滑杆上并与弹簧的上端连接;OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ=37°(取g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,光滑杆AB长为L,其B端固定一根劲度系数为k=100N/m,原长为l0=0.4m的轻质弹簧,质量为m=1kg的小球套在光滑杆上并与弹簧的上端连接;OO′为过B点的竖直轴,杆与水平面间的夹角始终为θ=37°(取g=10m/s2,sin37°=0.6,cos37°=0.8)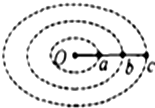 如图所示,a、b、c三个相同的小球系在同一根线上,oa=ab=bc,当它们绕O点在光滑水平面上以相同的角速度作匀速圆周运动时,三个小球的线速度之比为1:2:3..
如图所示,a、b、c三个相同的小球系在同一根线上,oa=ab=bc,当它们绕O点在光滑水平面上以相同的角速度作匀速圆周运动时,三个小球的线速度之比为1:2:3..