题目内容
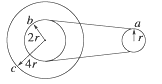
【题目】质量M=2kg的小车静止在光滑地面上,小车的左端紧靠竖直台阶,台阶的上表面与小车上表面等高,台阶的上表面光滑,右侧台阶与左侧等高,B点固定一个半径为R=0.2m的竖直光滑圆轨道。质量为m=2kg的小滑块P以初速度vo=4m/s向右运动并与静止在小车左端、质量也为m2=2kg小物块Q发生弹性碰撞,碰后小物块Q和小车一起向右滑动,且小车与右侧台阶相撞前恰好不滑离小车,小车与台阶碰后速度立即减为零。已知P、Q均可看作质点,B点左侧水平面光滑右侧水平面粗糙,若小物块速度足够大则能从B点向右滑上圆轨道经一个圆周再从B点向右滑离轨道。小物块Q与小车上表而及B点右侧水平面间的动摩擦因数均为p=0.5,重力加速度为g=10m/s",A点为右侧台阶的左端点。求:
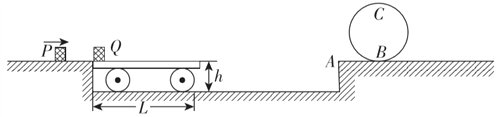
(1)碰后小物块Q的初速度;
(2)小车的长度及左右台阶间的距离;
(3)小物块Q冲上光滑圆轨道后能否做完整的因周运动,若能,请计算出小物块停止运动时距B点的距离;若不能,请求出小物块相对于小车净止时距A点的距离。
【答案】(1)4m/s;方向水平向右(2)0.8m;1.2m (3)0.3m
【解析】(1)小物块P、Q发生弹性碰撞,碰后速度分别为vP、vQ
由动量守恒知![]()
![]()
联立vP=0,vQ =4m/s 方向水平向右
(2)小物块Q在小车的上表面滑动的过程中,因受滑动摩擦力的作用,小物块作减速运动,小车做加速运动
则![]()
相对运动过程中系统的能量守恒,![]()
联立解得:![]() ,L=0.8m
,L=0.8m
小车向右滑行的加速度为![]()
小车向右运动的距离为![]()
左右台阶间的距离为![]()
(3)设小物块不能滑到与圆轨道的圆心等高处,则有![]()
上升高度为![]()
由于h=R,得小物块滑离轨道后以v=2m/s速度滑上小车,设在小车上滑行s距离时与小车速度相同,
由动量守恒和能量守恒得![]()
![]()
得![]() ,
,![]()
此过程中小车向左运动得最大距离![]()
此时小物块相对于A点的距离为![]()