Question

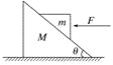
【题目】如图所示，质量为M，倾角为θ的光滑斜面静止在粗糙的水平面上，斜面上有一倒扣的直角三角形物块m，现对物块m施加一水平向左的推力F，使物块m与斜面一起向左做加速度为a的匀加速直线运动，已知重力加速度为g.求：

(1)物块对斜面的压力；

(2)水平推力F的大小；

(3)粗糙地面与斜面间的动摩擦因数．

Answer 1

【答案】(1) 　(2)mgtanθ＋ma　(3)

【解析】

（1）以m为研究对象，根据竖直方向受力平衡，结合牛顿第三定律，即可求出物块对斜面的压力；
（2）在对m受力分析，由牛顿第二定律列式即可求出力F；
（3）两物体没有发生相对滑动，具有相同的加速度，对整体受力分析并结合牛顿第二定律表示出加速度，即可求出动摩擦因数．

（1）以m为研究对象，竖直方向受力平衡，得：N=
根据牛顿第三定律，物块对斜面的压力为：N′=N=
（2）以m为研究对象，水平方向：F-Nsinθ=ma，得：F=mgtanθ+ma
（3）以m、M整体为研究对象：F-μ（m+M）=（M+m）a，可得：μ=