题目内容
如图所示,质量为M的小球B用长L=0.1m的细线悬于O点,恰好与水平地面Q点相切.质量为m=1.0kg的木块A与水平地面间的动摩擦因数μ=0.3,木块A从P点以速度v0=4.0m/s沿直线向右运动,与球B发生正碰,PQ=2.0m,碰撞时不损失机械能,且碰撞时间极短,碰撞后小球B向右摆起的最大角度为细线与竖直方向成60°角.(g=10m/s2)求:
①与小球B碰撞后木块A的速度;
②小球B的质量.

①与小球B碰撞后木块A的速度;
②小球B的质量.

A在PQ间做匀减速运动,由动能定理得:
-μmgxPQ=
mvA2-
mv02,
代入数据解得:vA=2m/s,
碰撞后小球B做圆周运动,机械能守恒,由机械能守恒定律得:
MvB2=MgL(1-cos60°),
代入数据解得:vB=1m/s,
A、B碰撞过程动量守恒,以A、B组成的系统为研究对象,以A的初速度方向为正方向,由动量守恒定律得:
mvA=mvA′+MvB,
碰撞过程机械能守恒,由机械能守恒定律得:
mvA2=
mvA′2+
MvB2,
代入数据解得:vA′=-1m/s,负号表示方向相反,方向向左,M=3kg;
答:①与小球B碰撞后木块A的速度为1m/s,方向向左;
②小球B的质量为3kg.
-μmgxPQ=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:vA=2m/s,
碰撞后小球B做圆周运动,机械能守恒,由机械能守恒定律得:
| 1 |
| 2 |
代入数据解得:vB=1m/s,
A、B碰撞过程动量守恒,以A、B组成的系统为研究对象,以A的初速度方向为正方向,由动量守恒定律得:
mvA=mvA′+MvB,
碰撞过程机械能守恒,由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:vA′=-1m/s,负号表示方向相反,方向向左,M=3kg;
答:①与小球B碰撞后木块A的速度为1m/s,方向向左;
②小球B的质量为3kg.

练习册系列答案
相关题目






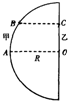 (3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?
(3)在某科技馆内放置了一个高大的半圆柱形透明物体,其俯视图如图所示,0为半圆的圆心.甲、乙两同学为了估测该透明体的折射率,进行了如下实验.他们分别站在A、O处时,相互看着对方,然后两人贴着柱体慢慢向一侧运动,到达B、C处时,甲刚好看不到乙.已知半圆柱体的半径为R,OC=0.6R,BC⊥OC,则半圆柱形透明物体的折射率为多少?