Question

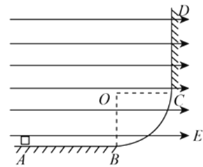
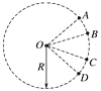
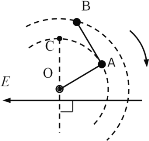
【题目】两根长为L的绝缘轻杆组成直角支架，电量分别为+q、-q的两个带电小球A、B固定在支架上，整个装置处在水平向左的匀强电场中，电场强度为E。在电场力之外的力作用下，整体在光滑水平面内绕竖直轴O以角速度ω顺时针匀速转动，图为其俯视图。不计两球之间因相互吸引而具有的电势能。试求：

（1）在支架转动一周的过程中，外力矩大小的变化范围。

（2）若从A球位于C点时开始计时，一段时间内（小于一个周期），电场力之外的力做功W等于B球电势能改变量，求W的最大值。

（3）在转动过程中什么位置两球的总电势能变化最快？并求出此变化率。

Answer 1

【答案】（1）0~qEL（2）W=－2qEL（3）OA杆与电场线平行时，电势能变化最快，变化率qEωL

【解析】

(1)设OA与电场线夹角，电场力矩与外力矩平衡，外力矩：

，

故外力矩大小的变化范围为0~qEL

(2)支架匀速转动，由动能定理可得

W+W电场力=0，

根据题意

W=ΔEpB，

得

W电场力=-ΔEpB，

电场力做功仅改变了B球电势能，所以A球电势能变化为零，则A球在这段时间初末应在同一个等势面上，根据B球前后位置关系，得：

W=-2qEL；

(3)因为电场力做功等于电势能改变量，所以电势能变化最快的位置应是电场力功率最大的位置。设OA与电场线夹角，由公式有

电场力功率：

，

显然在一周内θ=0或π时有最值，即OA杆与电场线平行时，电势能变化最快。为变化率qEωL

可能存在的另一类解法：

以OA与电场线平行，A在右端位置为t=0，以任意位置为零电势，均能得到整体电势能

Ep=qELsin(ωt)，

求导得电势能变化率=qEωLcos(ωt)，显然一周内ωt =0或π时有最值，即OA杆与电场线平行时，电势能变化最快。变化率qEωL。