题目内容
(12分)如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处飞出,最后落在水平面上,已知小球落地点C距B处的距离为3R.
求:小球对轨道口B处的压力为多大?
求:小球对轨道口B处的压力为多大?

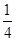 mg.
mg. 试题分析:设小球经过B点时速度为v0,则:
小球平抛的水平位移为:
x=
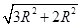 =
=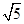 R (2分)
R (2分)v0=
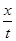 =
=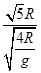 =
=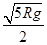 (3分)
(3分)对小球过B点时由牛顿第二定律得: F+mg=m
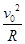 (3分)
(3分)解得 F=
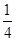 mg (2分)
mg (2分)由牛顿第三定律 F′=F=
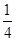 mg. (2分)
mg. (2分)点评:本题难度较小,在最高点由重力和弹力的合力提供向心力,根据平抛运动规律求得初速度,再由牛顿第二定律求解

练习册系列答案
相关题目
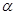 的正切tanα随时间t变化的图像是图1中的:
的正切tanα随时间t变化的图像是图1中的:


 ,,则物体将( )
,,则物体将( )
 ,方向竖直向下
,方向竖直向下 ,方向斜向下
,方向斜向下 ,方向斜向下
,方向斜向下 ,方向竖直向下
,方向竖直向下 平抛一个小球1,同时从地面以速度
平抛一个小球1,同时从地面以速度 竖直向上抛出一个小球2,两小球在空中相遇则:( )
竖直向上抛出一个小球2,两小球在空中相遇则:( ) 
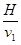 .(2) 从抛出到相遇所用时间为
.(2) 从抛出到相遇所用时间为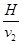
 (4).相遇时小球2上升高度
(4).相遇时小球2上升高度

