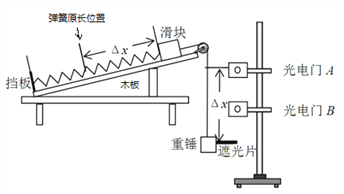
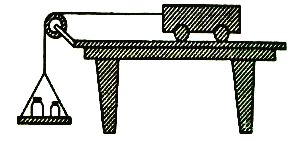
【题目】如图为“探究加速度与力、质量的关系”的实验装置,砂和砂桶的总质量为m,小车(含车内砝码)总质量为M,实验中用砂和砂桶总重力的大小作为细线对小车拉力的大小,小车运动加速度用a表示。


(1)实验中打点计时器应接____________电源。(选填“交流”或“直流”)。
(2)实验中,为了使细线对小车的拉力等于小车所受的合外力,先调节长木板一端滑轮的高度,使细线与长木板平行。接下来还需要进行的一项操作是(_____)
A.将长木板水平放置,让小车连着已经穿过打点计时器的纸带,给打点计时器通电,调节m的大小,使小车在砂和砂桶的牵引下运动,从打出的纸带判断小车是否做匀速运动
B.将长木板的一端垫起适当的高度,撤去纸带以及砂和砂桶,轻推小车,观察判断小车是否做匀速运动
C.将长木板的一端垫起适当的高度,让小车连着已经穿过打点计时器的纸带,撤去砂和砂桶,给打点计时器通电,轻推小车,从打出的纸带判断小车是否做匀速运动
(3) 在探究加速度与小车受力关系的过程中,要进行质量m和M的选取,以下最合理的一组是(_______)
A.M=400 g,m=10 g、15 g、20 g、25 g、30 g、40 g
B.M=400 g,m=20 g、40 g、60 g、80 g、100 g、120 g
C.M=100 g,m=10 g、15 g、20 g、25 g、30 g、40 g
D.M=100 g,m=20 g、40 g、60 g、80 g、100 g、120 g
(4) 下图是实验中得到的一条纸带,A、B、C、D、E、F、G为7个相邻的计数点,相邻的两个计数点之间还有四个点未画出。量出相邻的计数点之间的距离分别为:SAB=4.20 cm、SBC=4.65 cm、SCD=5.10 cm、SDE=5.54cm、SEF=6.00 cm、SFG=6.46 cm,已知打点计时器的工作周期为0.02s,则小车的加速度a=___________m/s2。(结果保留2位有效数字)

(5)在探究加速度与小车质量关系的过程中,应保持砂和砂桶的总质量不变,通过增减小车中砝码改变小车质量M,实验测出几组a、M数据,下列图线能直观合理且正确反映a-M关系的是_______。
A.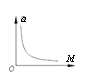 B.
B.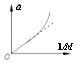 C.
C.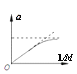 D.
D.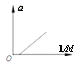

![]() (2)
(2)![]()
![]() ,解得
,解得![]() ;
;![]() ,此时弹簧的伸长量和F开始作用时的压缩量相同,弹簧的弹性势能改变量为零。由动能定理得
,此时弹簧的伸长量和F开始作用时的压缩量相同,弹簧的弹性势能改变量为零。由动能定理得![]() ,解得
,解得![]() 。
。