题目内容
 如图所示,长方形abcd长ad=0.6m,宽ab=0.3m,O、e分别是ad、bc的中点,以ad为直径的半圆内有垂直于纸面向里的匀强磁场(边界上无磁场),磁感应强度B=0.25T.一群不计重力、质量m=3×10-7kg、电荷量q=+2×10-3C的带电粒子.以速度v=5×102m/s沿垂直ad方向且垂直于磁场射入磁场区域,不考虑粒子的重力的相互作用.问:
如图所示,长方形abcd长ad=0.6m,宽ab=0.3m,O、e分别是ad、bc的中点,以ad为直径的半圆内有垂直于纸面向里的匀强磁场(边界上无磁场),磁感应强度B=0.25T.一群不计重力、质量m=3×10-7kg、电荷量q=+2×10-3C的带电粒子.以速度v=5×102m/s沿垂直ad方向且垂直于磁场射入磁场区域,不考虑粒子的重力的相互作用.问:(1)若从O点射入的带电粒子刚好沿Oe直线射出,求空间所加电场的大小和方向.
(2)若只有磁场时,某带电粒子从O点射入,求该粒子从长方形abcd射出的位置.
分析:(1)若从O点射入的带电粒子刚好沿Oe直线射出,电场力与洛伦兹力必须平衡,由平衡条件分析出电场的方向,列式求出电场强度的大小.
(2)若只有磁场时,粒子进入磁场后做匀速圆周运动,根据洛伦兹力提供向心力,先得到轨道半径,再找出圆心,确定半径并分析轨迹,确定粒子从长方形abcd射出的位置.
(2)若只有磁场时,粒子进入磁场后做匀速圆周运动,根据洛伦兹力提供向心力,先得到轨道半径,再找出圆心,确定半径并分析轨迹,确定粒子从长方形abcd射出的位置.
解答: 解:(1)若从O点射入的带电粒子刚好沿Oe直线射出,电场力与洛伦兹力必须平衡,由左手定则判断得知:洛伦兹力方向竖直向上,则电场力必须平行与bc向下,粒子带正电,电场方向也竖直向下.且有
解:(1)若从O点射入的带电粒子刚好沿Oe直线射出,电场力与洛伦兹力必须平衡,由左手定则判断得知:洛伦兹力方向竖直向上,则电场力必须平行与bc向下,粒子带正电,电场方向也竖直向下.且有
qE=qvB
解得,E=vB=5×102×0.25N=125N/C
(2)粒子进入磁场后做匀速圆周运动,根据洛伦兹力提供向心力,得
qvB=m
解得,r=
=
=0.3m=
ad
带电粒子进入磁场时所受的洛伦兹力向上,则粒子轨迹的圆心为a点.设粒子从ae弧上f点射出磁场
∵aO=af=r,Of=r,
∴△aOf是等边三角形,∠faO=60°
粒子经过磁场速度的偏向角θ=∠faO=60°
根据几何知识得:eg=r(1-cos60°)+(r-rsin60°)tan60°=(
-1)r=0.732×0.3m=0.22m
故带电粒子从e点上方距离e点0.22m射出磁场.
答:(1)空间所加电场的大小是125N/C,方向是平行与bc向下.
(2)该粒子从长方形abcd的bc边上e点上方距离e点0.22m射出磁场.
 解:(1)若从O点射入的带电粒子刚好沿Oe直线射出,电场力与洛伦兹力必须平衡,由左手定则判断得知:洛伦兹力方向竖直向上,则电场力必须平行与bc向下,粒子带正电,电场方向也竖直向下.且有
解:(1)若从O点射入的带电粒子刚好沿Oe直线射出,电场力与洛伦兹力必须平衡,由左手定则判断得知:洛伦兹力方向竖直向上,则电场力必须平行与bc向下,粒子带正电,电场方向也竖直向下.且有qE=qvB
解得,E=vB=5×102×0.25N=125N/C
(2)粒子进入磁场后做匀速圆周运动,根据洛伦兹力提供向心力,得
qvB=m
| v2 |
| r |
解得,r=
| mv |
| qB |
| 3×10-7×5×102 |
| 2×10-3×0.25 |
| 1 |
| 2 |
带电粒子进入磁场时所受的洛伦兹力向上,则粒子轨迹的圆心为a点.设粒子从ae弧上f点射出磁场
∵aO=af=r,Of=r,
∴△aOf是等边三角形,∠faO=60°
粒子经过磁场速度的偏向角θ=∠faO=60°
根据几何知识得:eg=r(1-cos60°)+(r-rsin60°)tan60°=(
| 3 |
故带电粒子从e点上方距离e点0.22m射出磁场.
答:(1)空间所加电场的大小是125N/C,方向是平行与bc向下.
(2)该粒子从长方形abcd的bc边上e点上方距离e点0.22m射出磁场.
点评:本题计算出半径后找到圆心,关键根据几何知识确定射出磁场的位置.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
如图所示,长方形abcd 长ad=0.6m,宽ab=0.3m,O、e分别是ad、bc的中点,以ad为直径的半圆内有垂直纸面向里的匀强磁场(边界上无磁场),磁感应强度B=0.25T。一群不计重力、质量m=3×10-7kg、电荷量q=+2×10-3C的带电粒子以速度v=5×102m/s沿垂直ad方向且垂直于磁场射入磁场区域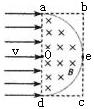
| A.从Od边射入的粒子,出射点全部分布在Oa边 |
| B.从aO边射入的粒子,出射点全部分布在ab边 |
| C.从Od边射入的粒子,出射点分布在Oa边和ab边 |
| D.从aO边射入的粒子,出射点分布在ab边和be边 |
 (2007?四川)如图所示,长方形abcd长ad=0.6m,宽ab=0.3m,O、e分别是ad、bc的中点,以ad为直径的半圆内有垂直纸面向里的匀强磁场(边界上无磁场),磁感应强度B=0.25T.一群不计重力、质量m=3×10-7kg、电荷量q=+2×10-3C的带电粒子以速度v=5×l02m/s沿垂直ad方向且垂直于磁场射人磁场区域( )
(2007?四川)如图所示,长方形abcd长ad=0.6m,宽ab=0.3m,O、e分别是ad、bc的中点,以ad为直径的半圆内有垂直纸面向里的匀强磁场(边界上无磁场),磁感应强度B=0.25T.一群不计重力、质量m=3×10-7kg、电荷量q=+2×10-3C的带电粒子以速度v=5×l02m/s沿垂直ad方向且垂直于磁场射人磁场区域( )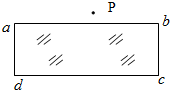 (2004?淮安二模)如图所示,长方形玻璃砖abcd的折射率n=1.55,在靠近ab面的一侧固定一枚大头针P,用眼睛在另外三个侧面分别观察大头针P的像,下列说法中正确的是( )
(2004?淮安二模)如图所示,长方形玻璃砖abcd的折射率n=1.55,在靠近ab面的一侧固定一枚大头针P,用眼睛在另外三个侧面分别观察大头针P的像,下列说法中正确的是( )