题目内容
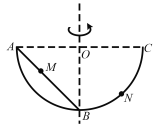
【题目】如图所示,ABC为在竖直平面内的金属半圆环,AC水平,AB为固定在AB两点间的直金属棒,在直棒上和圆环的BC部分分别套着两个相同的小环M、N,现让半圆环绕对称轴以角速度ω做匀速转动,半圆环的半径为R,小圆环的质量均为m,棒和半圆环均光滑,已知重力加速度为g,小环可视为质点,则M、N两环做圆周运动的线速度之比为
A.![]() B.
B.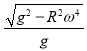
C.![]() D.
D.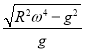
【答案】A
【解析】M点的小球受到重力和棒的支持力,在水平面内做匀速圆周运动,合力的方向沿水平方向,所以:Fn=mgtan 45°=mωvM,所以:![]() ①,同理,N点的小球受到重力和半圆环的支持力,在水平面内做匀速圆周运动,合力的方向沿水平方向,设ON与竖直方向之间的夹角为θ,Fn′=mgtan θ=mωvN,所以:
①,同理,N点的小球受到重力和半圆环的支持力,在水平面内做匀速圆周运动,合力的方向沿水平方向,设ON与竖直方向之间的夹角为θ,Fn′=mgtan θ=mωvN,所以:![]() ②,又:Fn′=mω2r③,r=Rsin θ④,联立②③④得:
②,又:Fn′=mω2r③,r=Rsin θ④,联立②③④得:![]() ⑤,所以:
⑤,所以:![]() ;故选A。
;故选A。

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目