题目内容
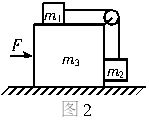
如图2所示,三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上.现给中间的小球B一个水平初速度v0,方向与绳垂直,小球相互碰撞时无机械能损失,轻绳不可伸长.求:
(1)当小球A、C第一次相碰时,小球B的速度；?
(2)当三个小球再次处在同一直线上时,小球B的速度；
(3)运动过程中小球A的最大动能EkA和此时两根绳的夹角θ；
(4)当三个小球处在同一直线上时,绳中的拉力F的大小.
（1）
解析:
(1)设小球A、C第一次相碰时,小球B的速度为vB,考虑到对称性及绳的不可伸长特性,小球A、C沿小球B初速度方向的速度也为vb,由动量守恒定律,得mv0=3mvB
(2)当三个小球再次处在同一直线上时,则由动量守恒定律和机械能守恒定律,得mv0=mvB+2mvA
解得
(三球再次处于同一直线)
vB=v0,vB=0(初始状态,舍去)
所以,三个小球再次处在同一直线上时,小球B的速度为
(负号表明与初速度反向).
(3)当小球A的动能最大时,小球B的速度为零,设此时小球A、C的速度大小为u,两根绳间夹角为θ(如图3),则仍由动量守恒定律和机械能守恒定律,得
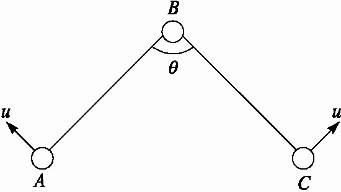
图3
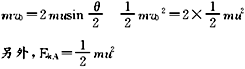
由此可解得,小球A的最大动能为
此时两根绳间夹角为θ=90°.
(4)小球A、C均以半径L绕小球B做圆周运动,当三个小球处在同一直线上时,以小球B为参考系(小球B的加速度为零,为惯性参考系),小球A(C)相对于小球B的速度均为v=｜vA-vB｜=v0，所以,此时绳中拉力大小为
练习册系列答案
相关题目
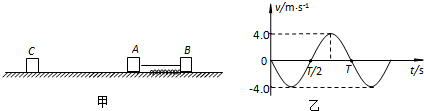（1）物体B运动速度的最大值；
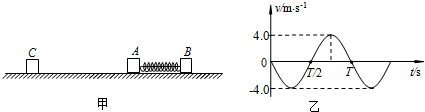时，物体A的速度?时间图象如图乙所示．求：
