Question

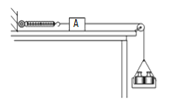
【题目】如图所示，长L＝3.41m的水平直杆BC，与高H＝0.2m的光滑细弯杆AB底部和足够长斜杆CD底部都平滑连接，CD与水平方向夹角θ＝37°．一质量m＝0.2kg的小环套在杆上，从最高点A由静止释放，沿细弯杆运动到B点时在小环上加一水平向右的外力F＝2N，至C点撤去，小环冲上斜杆CD．已知小环与杆BC、CD间动摩擦因数均为μ＝0.8．（g＝10m/s2，sin37°＝0.6，cos37°＝0.8）求：

（1）小环在B点时的速度vB大小；

（2）判断小环最终能否静止在斜杆上，通过表达式及计算加以说明；

（3）小环在斜杆CD上运动的时间。（小数点后保留两位）

Answer 1

【答案】（1）2m/s （2）由于G1＜fmax，可得小球能静止在斜杆上 （3）0.34s

【解析】

（1）对小环，从A到B的过程中，以水平面为零势面，因只有重力做功，由机械能守恒求解B点速度；

（2）在斜杆CD上，小球重力的沿斜面方向分力G1＝mgsin37°，与最大静摩擦力fmax＝μmgcos37°比较可知。

（3）对小环，在BC段，由牛顿第二定律求解加速度，根据vC2﹣vB2＝2a1L得vC，小环沿斜杆CD上滑过程中，由牛顿第二定律可得加速度，根据运动学公式求解时间。

（1）对小环，从A到B的过程中，以水平面为零势面，因只有重力做功，由机械能守恒，有：mvB2＝mgH

代入数据解得：vB＝ m/s＝2m/s

（2）在斜杆CD上，小球重力的沿斜面方向分力为：G1＝mgsin37°＝0.6mg

而最大静摩擦力为：fmax＝μmgcos37°＝0.64mg

由于G1＜fmax，可得小球能静止在斜杆上。

（3）对小环，在BC段，由牛顿第二定律知：

F﹣f1＝ma1

N1＝mg

f1＝μN1

代入数据解得：

a1＝m/s2＝2m/s2；

由vC2﹣vB2＝2a1L得：vC＝＝4.2m/s

小环沿斜杆CD上滑过程中，由牛顿第二定律可得：

mgsin37°+f2＝ma2

N2＝mgcos37°，

f2＝μN2

代入数据解得a2＝12.4m/s2

由vt＝vC﹣at

得t＝s＝0.34s