题目内容
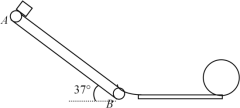
【题目】如图，有三个不同的斜轨道，高度相同，在水平方向的投影长度也相同，其中甲是直线轨道，乙是两个直线轨道通过一小段光滑圆弧连接的轨道，丙是曲线轨道。可视为质点的物体与三轨道的动摩擦因数相同，从轨道顶部由静止释放，到达底端时的速度大小分别为v1、v2和v3，则：
A. v1>v2>v3
B. v1=v2>v3
C. v1=v2<v3
D. v1=v2=v3
【答案】B
【解析】
设直轨道与水平面的夹角为θ，则下滑x时摩擦力的功：
，而xcosθ为轨道长度在水平面上的投影长度，可知甲乙两种情况下摩擦力的功相同，即Wf甲=Wf乙；根据动能定理：
可知，甲乙到达底端的速度相等v1=v2；对于丙图，可将整个曲线轨道分割为无数小段圆弧，根据圆周运动的规律，每一段小圆弧上滑块对轨道的压力都大于在直线斜轨道上运动时的压力，可知在曲线轨道上运动时摩擦力的功大于在直轨道上运动时摩擦力的功，由可知到达底端的速度小于在直轨道上运动时到达底端的速度，则v1=v2>v3，故选B.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】（6分）物理小组在一次探究活动中测量滑块与木板之间的动摩擦因数。实验装置如图，一表面粗糙的木板固定在水平桌面上，一端装有定滑轮；木板上有一滑块，其一端与电磁打点计时器的纸带相连，另一端通过跨过定滑轮的细线与托盘连接。打点计时器使用的交流电源的频率为50 Hz。开始实验时，在托盘中放入适量砝码，滑块开始做匀加速运动，在纸带上打出一系列小点。
（1）上图给出的是实验中获取的一条纸带的一部分：0、1、2、3、4、5、6、7是计数点，每相邻两计数点间还有4个打点（图中未标出），计数点间的距离如图所示。根据图中数据计算的加速度a= (保留三位有效数字)。
(2)回答下列两个问题：
为测量动摩擦因数，下列物理量中还应测量的有 。（填入所选物理量前的字母）
A．木板的长度l |
B．木板的质量m1 |
C．滑块的质量m2 |
D．托盘和砝码的总质量m3 |
E.滑块运动的时间t
滑块与木板间的动摩擦因数
＝ （用被测物理量的字母表示，重力加速度为g）.
