题目内容
【题目】如图，倾角为θ=37°的传送带AB长为l=16m，以v0=10m/s的速度顺时针转动，可视为质点的滑块从传送带顶端A点由静止释放，滑块与传送带之间的动摩擦因数为μ1=0.5，sin37°=0.6，cos37°=0.8，g=10m/s2，求：
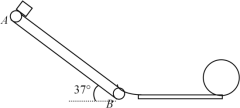
（1）滑块从A点运动至传送带底端B点所用的时间；
（2）若在传送带底端用一小段圆弧（长度不计）平滑连接一个水平轨道，滑块与轨道间的动摩擦因数为μ2=0.2，轨道右端连接一个半径R=2m的竖直光滑圆轨道，为使滑块在圆环内侧运动时不脱离轨道，水平轨道应该多长？
【答案】(1) 2s; (2)水平轨道的长度应满足：lCE≤11m或26m≤lCE≤36m
【解析】
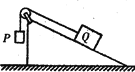
(1)在滑块速度达到传送带速度v0前，其受力分析如图。
在垂直于传送带平面方向物体处于静止状态，则有： 
物体受到的摩擦力大小为：
设物体运动到D点时速度等于v0，则：
从A到D，由牛顿第二定律得：
所以，有：
=10m/s2
从A到D所用时间为：
=1s
从A到D发生的位移：
=5m
同理，从D到B过程中，
所以，有：
=2m/s2
DB间的距离x2=l-x1=11m
设再用时间t2滑块运动至传送带底端，则有：
解得： t2=1s
所以，滑块从A点运动至传送带底端B点所用的时间为：t=t1+t2=2s
(2)由(1)可知，滑块运动至B点时的速度为v，有：
=12m/s
①若滑块能滑到圆轨道最高点F，则在最高点由牛顿第二定律得：
， 其中 FNF≥0 ，
有：
m/s
从B至圆轨道最高点，由动能定理有：
， 解得：lCE≤11m
②若滑块能到达的最高点在与圆心等高的位置以下，则滑块也不脱轨。
则由动能定理得：
，式中h＇为滑块在圆环内上升的高度
因为： 0≤h＇≤R=2m ，
解得： 26m≤lCE≤36m
综合①②可知，要使滑块不脱离圆环，水平轨道的长度应满足：
lCE≤11m 或 26m≤lCE≤36m
优学名师名题系列答案
