题目内容
18. 如图所示,整个装置处于静止状态,A、B两球由一根跨过定滑轮的轻绳相连接,A为一带孔小球,穿在光滑固定的竖直杆OD上,且A球与斜面不接触.B与斜面体的接触面光滑,C处滑轮摩擦不计,C、B之间的绳与竖直方向成30°角,C、A之间的绳与斜面平行,斜面倾角为θ=30°,则A、B两球的质量比为( )
如图所示,整个装置处于静止状态,A、B两球由一根跨过定滑轮的轻绳相连接,A为一带孔小球,穿在光滑固定的竖直杆OD上,且A球与斜面不接触.B与斜面体的接触面光滑,C处滑轮摩擦不计,C、B之间的绳与竖直方向成30°角,C、A之间的绳与斜面平行,斜面倾角为θ=30°,则A、B两球的质量比为( )| A. | 4:$\sqrt{3}$ | B. | 1:1 | C. | $\sqrt{3}$:1 | D. | 1:$\sqrt{3}$ |
分析 先对B球受力分析,运用共点力平衡条件求出细线的拉力T;再对A球受力分析,再次运用共点力平衡条件求出B球的质量.
解答 解:先对B球受力分析,受重力、支持力和拉力,再对A球受力分析,受重力、拉力向右的支持力,如图
根据共点力平衡条件,有
对B球:T=$\frac{mg}{cos30°}$ ①
对A球
水平方向:Tcos30°=FN ②
竖直方向:Tsin30°=Mg ③
由①②③解得
m=$\sqrt{3}$M
故选:D.
点评 本题关键是分别对A、B两个球进行受力分析,然后根据共点力平衡条件,并结合正交分解法或合成法分析求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.在高度为H的同一位置,向水平方向同时抛出两个小球A和B,如果VA>VB,则下列说法中正确的是( )
| A. | A球落地时间小于B球落地时间 | |
| B. | A球射程大于B球的射程 | |
| C. | 如果两球在飞行中遇到一堵竖直的墙壁,两球击中墙的高度可能相同 | |
| D. | 在空中飞行的任意相等的时间内,两球的速度增量总是不同的 |
6. 某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标系上,如图中的a、b、c所示,根据图线可知( )
某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标系上,如图中的a、b、c所示,根据图线可知( )
 某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标系上,如图中的a、b、c所示,根据图线可知( )
某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在了同一坐标系上,如图中的a、b、c所示,根据图线可知( )| A. | 反映变化Pr的图线是c | B. | 电源电动势为8 V | ||
| C. | 电源内阻为1Ω | D. | 当电流为1A时,电源的效率为50% |
3.关于自由落体运动,下列说法正确的是( )
| A. | 质量大的物体自由下落时的加速度大 | |
| B. | 雨滴下落的过程是自由落体运动 | |
| C. | 在自由落体运动过程中,不同质量的物体运动规律相同 | |
| D. | 从水平飞行着的飞机上释放的物体将做自由落体运动 |
10.关于质点的判断正确的是( )
| A. | 质点是指那些形状很小的物体 | |
| B. | 平直的公路上行驶的汽车,研究其从甲地到乙地所需的时间时,汽车可视为质点 | |
| C. | 北京开往上海的火车,研究其过一座长200米桥梁的时间时,火车可视为质点 | |
| D. | 研究杂技演员在做空翻动作的相关问题时,可将杂技演员视为质点 |
 如图所示,一束电子从x轴上的A点以平行于y轴的方向射入第一象限区域,射入的速度为v0,电子质量为m,电荷量为e.为了使电子束通过y轴上的B点,可在第一象限的某区域加一个沿x轴正方向的匀强电场,此电场的电场强度为E,电场区域沿x轴方向为无限长,沿y轴方向的宽度为s,且已知OA=L,OB=2s,求
如图所示,一束电子从x轴上的A点以平行于y轴的方向射入第一象限区域,射入的速度为v0,电子质量为m,电荷量为e.为了使电子束通过y轴上的B点,可在第一象限的某区域加一个沿x轴正方向的匀强电场,此电场的电场强度为E,电场区域沿x轴方向为无限长,沿y轴方向的宽度为s,且已知OA=L,OB=2s,求
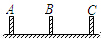 一辆汽车在平直的公路上做匀变速直线运动,该公路上每隔15m安装一个路标,如图所示,汽车通过AB两相邻路标用了2s,通过BC两路标用了3s,求汽车通过A、B、C三个路标时的速度.
一辆汽车在平直的公路上做匀变速直线运动,该公路上每隔15m安装一个路标,如图所示,汽车通过AB两相邻路标用了2s,通过BC两路标用了3s,求汽车通过A、B、C三个路标时的速度.