��Ŀ����
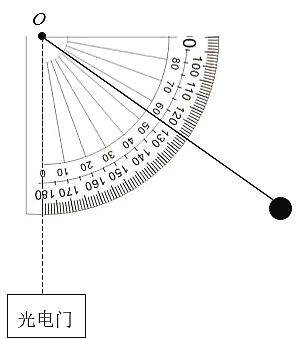
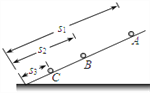
����Ŀ��٤�������о����������˶�ʱ���������µ�ʵ�飺����һ��ͭ���������С���ɺ��Բ��ƣ���б�����ɾ�ֹ��ʼ���£����������ϰٴΣ�����ij��ʵ��٤�������������ģ���б������ȡ����λ��A��B��C����С��ֱ���A��B��C���£���ͼ��ʾ����A��B��C��б��˵ľ���ֱ�Ϊs1��s2��s3��С����A��B��C�˶���б��˵�ʱ��ֱ�Ϊt1��t2��t3��С����A��B��C�˶���б���ʱ���ٶȷֱ�Ϊ��1����2����3�����й�ϵʽ����ȷ��������٤��������֤��С���ع⻬б�����µ��˶����ȱ���ֱ���˶����ǣ�������
A. ![]() B.
B. ![]()
C. s1-s2=s2-s3 D. ![]()
���𰸡�B
��������A. ��v=at�ɵ���a=v/t�����������еļ��ٶ���ͬ����Aʽ��ȷ�����Dz��ǵ�ʱ٤��������֤���ȱ���ֱ���˶��Ľ�������A����
С����б���������˶���λ�Ʋ�ͬ��ĩ�ٶ�һ����ͬ����A����
B.��![]() �ɵã�
�ɵã� ![]() �����������еļ��ٶ���ͬ����Bʽ��ȷ��Ҳ�ǵ�ʱ٤��������֤���ȱ���ֱ���˶��Ľ��ۣ�B��ȷ��
�����������еļ��ٶ���ͬ����Bʽ��ȷ��Ҳ�ǵ�ʱ٤��������֤���ȱ���ֱ���˶��Ľ��ۣ�B��ȷ��
C.��������λ��A��B��C������ѡȡ������һ������s1-s2=s2-s3�Ĺ�ϵ����C����
D.С����б���ȼ����˶�����ͬ��ƽ���ٶȲ�ͬ��ĩ�ٶȵ�һ�������һ��ʱ���ڵ�ƽ���ٶȣ��������D������
��ѡ��B.