题目内容
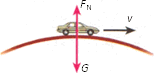
如图所示，汽车过拱形桥时的运动可以看做匀速圆周运动，质量为m的汽车以速度v过桥，桥面的圆弧半径为R，重力加速度为g，则汽车通过桥面最高点时对桥面的压力大小为（ ）| A、mg | ||
B、
| ||
C、mg-
| ||
D、mg+
|
分析：汽车过拱桥最高点时，靠重力和支持力的合力通过向心力，根据牛顿第二定律求出支持力的大小，从而得出汽车对桥顶的压力．
解答：解：根据牛顿第二定律得：
mg-N=m
，
解得支持力为：N=mg-m
，
根据牛顿第三定律知，汽车通过桥面最高点时对桥面的压力大小为：
N′=mg-m
．故C正确，A、B、D错误．
故选：C．
mg-N=m
| v2 |
| R |
解得支持力为：N=mg-m
| v2 |
| R |
根据牛顿第三定律知，汽车通过桥面最高点时对桥面的压力大小为：
N′=mg-m
| v2 |
| R |
故选：C．
点评：解决本题的关键知道汽车做圆周运动向心力的来源，结合牛顿第二定律进行求解．
练习册系列答案
相关题目
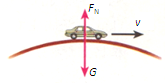如图所示，汽车在拱形桥上以速度v前进，下列关于汽车过桥顶的说法中正确的是（ ）
如图所示，汽车过拱形桥时的运动可以看做匀速圆周运动，质量为1吨的汽车以20m/s的速度过桥，桥面的圆弧半径为500m，g取9.8m/s2，则汽车过桥面顶点时对桥面的压力是（ ）
