题目内容
11.某同学利用如甲图所示的实验装置,探究物块在水平桌面上的运动规律,静止物块在重物的牵引下开始匀加速运动,重物落地后,物块再匀减速运动一段距离停在桌面上(尚未到达滑轮处).从纸带上便于测量的点开始取计数点,相邻计数点间都有4个点画出,对应距离如乙图所示(计数点序号对应运动的时间先后顺序).打点频率为50Hz.
(1)通过分析纸带数据,可知重物在相邻两计数点6和7之间某时落地.
(2)计数点4对应的速度大小为0.801m/s,计数点6对应的速度大小为1.20m/s.(保留3位有效数字).
(3)该运动过程的加速与减速时间之比为$\frac{801}{800}$(用分数表示).
分析 (1)由纸带两个点之间的时间相同,若位移逐渐增大,表示物体做加速运动,若位移逐渐减小,则表示物体做减速运动;
(2)用平均速度代替瞬时速度的方法求解瞬时速度;
(3)根据连续相等时间内的位移之差是一恒量求出匀加速和匀减速运动的加速度大小,结合速度时间公式求出加速和减速的时间之比.
解答 解:(1)从纸带上的数据分析得知:在点计数点6之前,两点之间的位移逐渐增大,是加速运动,在计数点7之后,两点之间的位移逐渐减小,是减速运动,所以物块在相邻计数点6和7之间某时刻开始减速,即重物在相邻计数点6和7之间某时落地.
(2)计数点对应的速度为:${v}_{4}=\frac{{x}_{35}}{2T}=\frac{(7.01+9.00)×1{0}^{-2}}{0.2}$m/s=0.801m/s,
匀加速运动的加速度为:${a}_{1}=\frac{{x}_{35}-{x}_{13}}{4{T}^{2}}$=$\frac{(7.01+9.00-5.01-3.00)×1{0}^{-2}}{4×0.01}$=2.00m/s2,
则有:v6=v4+a•2T=0.801+2×0.2≈1.20m/s.
(3)匀减速运动的加速度大小为:
${a}_{2}=\frac{{x}_{79}-{x}_{1011}}{4{T}^{2}}$=$\frac{(10.60+8.61-6.60-4.60)×1{0}^{-2}}{4×0.01}$=$\frac{8.01}{4}m/{s}^{2}$
根据v=at知,加速和减速的时间之比等于加速度之反比,即$\frac{{t}_{1}}{{t}_{2}}=\frac{{a}_{2}}{{a}_{1}}=\frac{801}{800}$.
故答案为:(1)6,7,(2)0.801,1.20,(3)$\frac{801}{800}$.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.

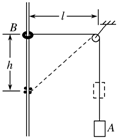 如图所示,物体A的质量为M=50kg,物体B的质量为m=22kg,通过绳子连接在一起,物体B套在光滑的竖直杆上,开始时连接物体B的绳子处于水平,长度l=4m,现从静止释放物体B,物体B下降h=3m时的速度为( )(不计定滑轮和空气的阻力,取g=10m/s2)
如图所示,物体A的质量为M=50kg,物体B的质量为m=22kg,通过绳子连接在一起,物体B套在光滑的竖直杆上,开始时连接物体B的绳子处于水平,长度l=4m,现从静止释放物体B,物体B下降h=3m时的速度为( )(不计定滑轮和空气的阻力,取g=10m/s2)| A. | v=$\frac{2\sqrt{10}}{3}$m/s | B. | v=2$\sqrt{2}$m/s | C. | v=$\frac{2\sqrt{10}}{5}$m/s | D. | v=$\frac{6\sqrt{2}}{5}$m/s |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
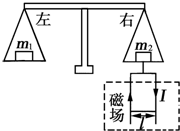 如图所示的等臂天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽为l,共N匝,线圈的下部悬在匀强磁场中,磁场方向垂直纸面.当线圈中通有电流I(方向如图)时,天平平衡;当电流反向(大小不变)时,右边再加上质量为m的砝码后,天平重新平衡.由此可知( )
如图所示的等臂天平可用来测定磁感应强度.天平的右臂下面挂有一个矩形线圈,宽为l,共N匝,线圈的下部悬在匀强磁场中,磁场方向垂直纸面.当线圈中通有电流I(方向如图)时,天平平衡;当电流反向(大小不变)时,右边再加上质量为m的砝码后,天平重新平衡.由此可知( )| A. | 磁感应强度的方向垂直纸面向外,大小为$\frac{mg}{NIl}$ | |
| B. | 磁感应强度的方向垂直纸面向外,大小为$\frac{mg}{2NIl}$ | |
| C. | 磁感应强度的方向垂直纸面向里,大小为$\frac{mg}{NIl}$ | |
| D. | 磁感应强度的方向垂直纸面向里,大小为$\frac{mg}{2NIl}$ |
| A. | 加速度 | B. | 速度 | ||
| C. | 平均速度 | D. | 位移(相对于抛出点) |
| A. | 中国乒乓球队队员马林在第29届北京奥运会上获得男单的金牌,在研究他发出的乒乓球时 | |
| B. | 研究从常德开往长沙的列车的运动时间时 | |
| C. | 研究哈雷慧星绕太阳公转时 | |
| D. | 用GPS定位系统研究汽车位置时 |
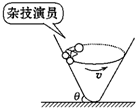 “飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶 面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为θ,车和人的总质量为m,做圆周运动的半径为r,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
“飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶 面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为θ,车和人的总质量为m,做圆周运动的半径为r,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )| A. | 人和车的速度为$\sqrt{grtanθ}$ | B. | 桶面对车的弹力为$\frac{mg}{sinθ}$ | ||
| C. | 桶面对车的弹力为$\frac{mg}{cotθ}$ | D. | 人和车的速度为$\sqrt{grsinθ}$ |
| A. | 电子伏是能量的单位 | B. | 电子伏是电势差的单位 | ||
| C. | 1eV=1.60×1019J | D. | 1eV=1.60×10-19J |