Question

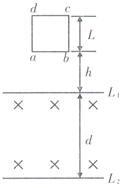
【题目】如图所示，相距为L的两条足够长的平行金属导轨，与水平面的夹角为θ，金属导轨电阻不计。导轨上有质量为m、电阻为R的两根相同的导体棒，导体棒MN上方轨道粗糙、导体棒MN所在位置及下方轨道光滑，整个空间存在垂直于导轨平面的匀强磁场，磁感应强度为B.将两根导体棒同时释放后，观察到导体棒MN下滑而EF保持静止，当MN下滑x距离后恰好达到最大速度时，EF与轨道间的摩擦力也刚好达到最大静摩擦力。求：

（1）导体棒MN的最大速度及EF所受最大静摩擦力各是多少；

（2）如果导体棒MN从静止释放沿导轨下滑x距离后恰好达到最大速度，这一过程回路中通过导体棒MN横截面的电荷量及导体棒MN产生的电热是多少。

Answer 1

【答案】（1）v= ；2mgsin θ．

（2） ,Q=mgxsin θ－

【解析】

根据“当MN下滑x距离后恰好达到最大速度时，EF与轨道间的摩擦力也刚好达到最大静摩擦力。”“回路中通过导体棒MN横截面的电荷量及导体棒MN产生的电热是多少。”可知，本题考查电磁感应金属棒在斜面上切割磁感线运动的收尾速度和能量转化问题，根据速度最大时两金属棒受力平衡，利用平均电流求电量，能量转化与守恒分别列方程，求解即可。

（1）由题意可知，导体棒MN切割磁感线，产生的感应电动势为E＝BLv，回路中的电流I＝，MN受到的安培力F＝BIL＝，

故MN沿斜面做加速度减小的加速运动，

当MN受到的安培力大小等于其重力沿轨道方向的分力时，速度达到最大值，此后MN做匀速运动．

故导体棒MN受到的最大安培力为mgsin θ，导体棒MN的最大速度为v=

由于当MN下滑速度最大时，EF与轨道间的摩擦力刚好达到最大静摩擦力，由力的平衡知识可知EF与轨道之间的最大静摩擦力为2mgsin θ.

（2）这一过程回路中通过导体棒MN横截面的电荷量q=Δt =

设这一过程回路中导体棒MN产生的电热是Q，由能量守恒定律有

mgsinθ·x＝mv2＋2Q

解得Q=mgxsinθ－