题目内容
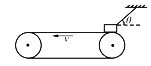
【题目】在水平面上，平放一半径为R的光滑半圆管道，管道处在方向竖直、磁感应强度为B的匀强磁场中，另有一个质量为m、带电荷量为＋q的小球．
（1）当小球从管口沿切线方向以某速度射入，运动过程中恰不受管道侧壁的作用力，求此速度v0；
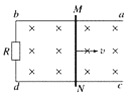
（2）现把管道固定在竖直面内，且两管口等高，磁场仍保持和管道平面垂直，如图所示．空间再加一个水平向右、场强E＝
的匀强电场(未画出)．若小球仍以v0的初速度沿切线方向从左边管口射入，求小球：
①运动到最低点的过程中动能的增量；
②在管道运动全程中获得的最大速度．
【答案】（1）
（2）①2mgR②
【解析】（1）小球在水平面上只受到洛伦兹力作用，故
解得： 
。
（2）①小球在管道运动时，洛伦兹力始终不做功，对小球运动到最低点的过程，由动能定理可以得到： 
由题目已知： 
联合以上两式可以得到：动能增量
。
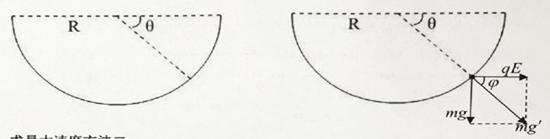
②当小球到达管道中方位角为
的位置（如图所示）时，应用动能定理，有：
即： 
对函数
求极值，可得
时， 
所以
练习册系列答案
相关题目
