题目内容
13.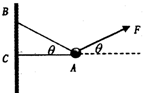 如图所示,小球的质量为m=5kg,两根轻绳AB和AC的一端连接于竖直的墙上,另一端系于小球上,在小球上另施加一个方向与水平面成θ=30°的拉力F,若要使两绳都保持伸直(伸直时两绳夹角也为30°),g取10m/s2,求拉力F的大小范围.
如图所示,小球的质量为m=5kg,两根轻绳AB和AC的一端连接于竖直的墙上,另一端系于小球上,在小球上另施加一个方向与水平面成θ=30°的拉力F,若要使两绳都保持伸直(伸直时两绳夹角也为30°),g取10m/s2,求拉力F的大小范围.
分析 若AC绳恰好无拉力时,F有最小值.若AB绳恰好无拉力时,F有最大值.对A物体受力分析,受到拉力F,重力mg,两根细绳的拉力F1、F2,根据共点力平衡条件列方程,求F的最大值和最小值,然后得到F的范围.
解答  解:当AC尽管被拉直但恰好无拉力时,F有最小值F1.对小球受力分析如图1所示,由T和F1的合力与小球的重力mg等大、反向,由力的平行四边形可得:mg=2F1cos(90°-θ)
解:当AC尽管被拉直但恰好无拉力时,F有最小值F1.对小球受力分析如图1所示,由T和F1的合力与小球的重力mg等大、反向,由力的平行四边形可得:mg=2F1cos(90°-θ)
解得:F1=$\frac{mg}{2sinθ}$=50N
当AB尽管被拉直但恰好无拉力时,F有最小值F2.对小球受力分析如图2所示,将拉力F2沿水平和竖直两个方向分解,由竖直方向受力平衡得:
F2sinθ=m
解得:F2=$\frac{mg}{sinθ}$=100N
故拉力F的大小范围为:50N≤F≤100N.
答:拉力F的大小范围为 50N≤F≤100N.
点评 本题关键是找出F最大和最小的两种临界情况进行讨论,再对小球受力分析,列平衡方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3. 物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=1m,BC=2m.且物体通过AB、BC、CD所用时间都是1秒,则下列说法正确的是( )
物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=1m,BC=2m.且物体通过AB、BC、CD所用时间都是1秒,则下列说法正确的是( )
 物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=1m,BC=2m.且物体通过AB、BC、CD所用时间都是1秒,则下列说法正确的是( )
物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=1m,BC=2m.且物体通过AB、BC、CD所用时间都是1秒,则下列说法正确的是( )| A. | 可求得OA=0.5m | |
| B. | 可以求得CD=4m | |
| C. | 可以求出物体加速度的大小是a=1m/s2 | |
| D. | 可求得A点的速度v=0.5m/s |
4.关于温度和内能的下列说法中正确的是( )
| A. | 温度是物体内能的标志 | |
| B. | 当物体内的一个分子的运动增大时,该物体的温度一定升高 | |
| C. | 只有热传递才能改变物理的内能 | |
| D. | 做功和热传递都能改变物体的内能 |
1.以下叙述正确的是( )
| A. | 库仑提出了分子电流假说 | |
| B. | 首先发现电流周围存在磁场的著名科学家是奥斯特 | |
| C. | 首先提出磁场对运动电荷有力的作用的科学家是安培 | |
| D. | 感应电流遵从楞次定律所描述的方向,这是能量守恒定律的必然结果 |
8.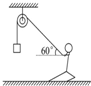 如图所示,重力为500N的人通过跨过定滑轮的轻绳拉起重力为200N的物体,当绳与水平面成60°角时,物体静止.不计滑轮与绳的摩擦,关于地面对人的支持力和摩擦力( )
如图所示,重力为500N的人通过跨过定滑轮的轻绳拉起重力为200N的物体,当绳与水平面成60°角时,物体静止.不计滑轮与绳的摩擦,关于地面对人的支持力和摩擦力( )
 如图所示,重力为500N的人通过跨过定滑轮的轻绳拉起重力为200N的物体,当绳与水平面成60°角时,物体静止.不计滑轮与绳的摩擦,关于地面对人的支持力和摩擦力( )
如图所示,重力为500N的人通过跨过定滑轮的轻绳拉起重力为200N的物体,当绳与水平面成60°角时,物体静止.不计滑轮与绳的摩擦,关于地面对人的支持力和摩擦力( )| A. | 摩擦力大小为100$\sqrt{3}$N,水平向左 | |
| B. | 支持力大小为400N | |
| C. | 若人向右移动后物体仍静止,地面对人的支持力将变大 | |
| D. | 若人向右移动后物体仍静止,地面对人的摩擦力将变大 |
18.如图所示是在高速公路是哪个用测速仪测量车速的示意图,测速仪发出并接收超声波脉冲信号,根据发出和接收到信号间的时间差测出被测物体的速度.图中P1、P2是测速仪发出的超声波信号,n1、n2分别是P1、P2由汽车反射回来的信号,设测速仪匀速扫描,P1、P2之间的时间间隔△t=1.0s,超声波在空气中的传播速度是v=340m/s,若汽车的运动情况是( )(汽车运动方向沿车与测速仪的连线)


| A. | 汽车在靠近超声波测速仪,速度大小为17.0m/s | |
| B. | 汽车在靠近超声波测速仪,速度大小为17.9m/s | |
| C. | 汽车在远离超声波测速仪,速度大小为17.0m/s | |
| D. | 汽车在远离超声波测速仪,速度大小为17.9m/s |
5.如图所示为某次测量电源的电动势和内阻所作的U-I图象,有关这个图象的说法正确的是( )
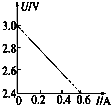

| A. | 纵轴截距表示待测电源的电动势,即E=3v | |
| B. | 横轴截距表示短路电流,即I短=0.6A | |
| C. | 根据r=$\frac{E}{{I}_{短}}$,计算出待测电阻内阻为5Ω. | |
| D. | 根据r=$\frac{△U}{△I}$,计算出待测电源内阻为1Ω. |
2.汽车从静止开始作匀变速直线运动,第4秒末关闭发动机,再经6秒停止,汽车一共行驶了40米则( )
| A. | 在运动过程中的最大速度为8m/s | |
| B. | 在运动过程中的最大速度为5m/s | |
| C. | 加速阶段的加速度的大小为2m/s2 | |
| D. | 减速阶段的加速度的大小为1.5m/s2 |
 如图所示,水平放置的平行金属板A和B间的距离为d,极长L=$\sqrt{3}$d,B板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成60°角,K与N间的距离$\overline{KN}$=a.现有一质量为m、电荷量为q的带正电的粒子,从AB的中点O以平行于金属板方向OO′的速度v0射入,不计粒子的重力.现在A、B板上加一恒定电压,则该粒子穿过金属板后恰好穿过小孔K:
如图所示,水平放置的平行金属板A和B间的距离为d,极长L=$\sqrt{3}$d,B板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成60°角,K与N间的距离$\overline{KN}$=a.现有一质量为m、电荷量为q的带正电的粒子,从AB的中点O以平行于金属板方向OO′的速度v0射入,不计粒子的重力.现在A、B板上加一恒定电压,则该粒子穿过金属板后恰好穿过小孔K: