题目内容
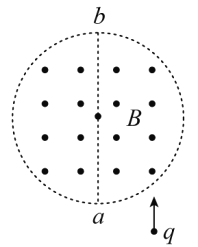
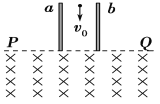
【题目】如图所示，a、b为竖直正对放置的两平行金属板，其中a板带正电、两板间的电压为U。在金属板下方存在一有界的匀强磁场，磁场的上边界为与两金属板下端重合的水平面PQ，PQ下方的磁场范围足够大，磁场的磁感应强度大小为B。一比荷为
的带正电粒子以速度v0从两板中间位置沿与a、b平行方向射入两板间的偏转电场，不计粒子重力。粒子通过偏转电场后从PQ边界上的M点进入磁场，运动一段时间后又从PQ边界上的N点射出磁场，设M、N两点距离为x（M、N点在图中未画出）。则以下说法中正确的是（ ）
A.只减小磁感应强度B的大小，则x减小
B.只增大初速度v0的大小，则x不变
C.只增大带电粒子的比荷，则x增大
D.只减小偏转电场的电压U的大小，则x不变
【答案】D
【解析】
设
、
平行金属板的长度为
，板间距离为
；粒子的运动轨迹如图所示：
粒子在电场中做类平抛运动，粒子离开电场时的速度：
粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律得：
、
两点间的距离：
AB．只减小磁感应强度B或只增大初速度v0，都会使x增大，AB错误；
C．只增大带电粒子的比荷
时，x会减小，C错误；
D．x与偏转电场的电压U无关，故x不变，D正确。
故选D。
练习册系列答案
相关题目
