题目内容
16.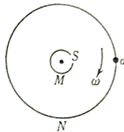 如图是德国物理学家史特恩设计的最早测定气体分子速率的示意图:M、N是两个共轴圆筒,外筒半径为R,内筒半径很小可忽略,筒的两段封闭,两筒之间抽成真空,两筒以相同角速度ω绕O匀速转动,M 筒开有与转轴平行的狭缝S,且不断沿半径方向向外射出速率为v1和v2的分子,分子到达N筒后被吸附,如果R、v1、v2保持不变,ω取一合适值,则( )
如图是德国物理学家史特恩设计的最早测定气体分子速率的示意图:M、N是两个共轴圆筒,外筒半径为R,内筒半径很小可忽略,筒的两段封闭,两筒之间抽成真空,两筒以相同角速度ω绕O匀速转动,M 筒开有与转轴平行的狭缝S,且不断沿半径方向向外射出速率为v1和v2的分子,分子到达N筒后被吸附,如果R、v1、v2保持不变,ω取一合适值,则( )| A. | 当|$\frac{R}{{v}_{1}}-\frac{R}{{v}_{2}}$|=n$\frac{2π}{ω}$时,分子落在同一狭条上(n取正整数) | |
| B. | 当$\frac{R}{{v}_{1}}+2\frac{R}{{v}_{2}}=n\frac{2π}{ω}$时,分子落在同一个狭条上(n取正整数) | |
| C. | 只要时间足够长,N筒上到处都落有分子 | |
| D. | 分子不可能落在N筒上某两处且与S平行的狭条上 |
分析 微粒从窄缝射出后沿筒的半径方向做匀速直线运动,同时N筒以角速度ω绕轴线转动,当微粒到达N筒时,二者运动时间相等,通过时间相等关系求解作出判断.
解答 解:微粒从M到N运动时间t=$\frac{R}{v}$,对应N筒转过角度θ=ωt=$\frac{ωR}{v}$,即如果以v1射出时,转过角度:θ1=ωt=$\frac{ωR}{{v}_{1}}$,如果以v2射出时,转过角度:θ2=ωt=$\frac{ωR}{{v}_{2}}$,只要θ1、θ2不是相差2π的整数倍,即当$|\frac{R}{{v}_{1}}-\frac{R}{{v}_{2}}|≠n\frac{2π}{ω}$时(n为正整数),分子落在不同的两处与S平行的狭条上,故A正确,D错误;
若相差2π的整数倍,则落在一处,即当$\frac{R}{{v}_{1}}-\frac{R}{{v}_{2}}=n\frac{2π}{ω}$时(n为正整数),分子落在同一个狭条上.故B错误;
若微粒运动时间为N筒转动周期的整数倍,微粒只能到达N筒上固定的位置,因此,故C错误.
故选:A
点评 解答此题一定明确微粒运动的时间与N筒转动的时间相等,在此基础上分别以v1、v2射出时来讨论微粒落到N筒上的可能位置.

练习册系列答案
相关题目
7. 如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,则下列说法正确的是( )
如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,则下列说法正确的是( )
 如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,则下列说法正确的是( )
如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,则下列说法正确的是( )| A. | 小球通过最高点时最小速度vmin=$\sqrt{g(R+r)}$ | |
| B. | 小球通过最高点时最小速度vmin=0 | |
| C. | 小球在水平线ab以下的管道中运动时,内侧管壁对小球可能有作用力 | |
| D. | 小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力 |
4.两颗人造地球卫星,它们质量的比m1:m2=1:2,它们运行的线速度的比是v1:v2=1:2,那么下列说法不正确的是( )
| A. | 它们所受向心力的比为1:32 | B. | 它们运行的轨道半径之比为4:1 | ||
| C. | 它们运行的周期比为1:8 | D. | 它们运动的向心加速度的比为1:16 |
5.单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中错误的是( )
| A. | 无论增大入射光的频率还是增加入射光的强度,金属的逸出功都不变 | |
| B. | 只延长入射光照射时间,光电子的最大初动能将增加 | |
| C. | 只增大入射光的频率,光电子的最大初动能将增大 | |
| D. | 只增大入射光的强度,单位时间内逸出的光电子数目将增多 |
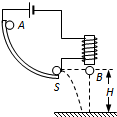 如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开接触开关S,被电磁铁吸住的小球B同时自由下落,改变整个装置的高度H做同样的实验,发现同一高度的A、B两个小球总是同时落地,该现象说明了A球在离开轨道后自由落体运动.
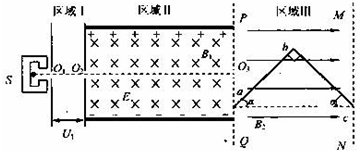
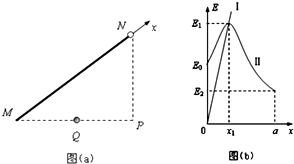
如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开接触开关S,被电磁铁吸住的小球B同时自由下落,改变整个装置的高度H做同样的实验,发现同一高度的A、B两个小球总是同时落地,该现象说明了A球在离开轨道后自由落体运动.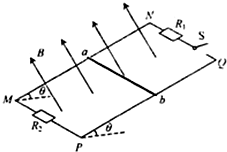 如图所示,足够长的平行金属导轨MN、PQ平行放置,间距为L,与水平面成θ角,导轨与固定电阻R1和R2相连,且R1=R2=R.R1支路串联开关S,原来S闭合,匀强磁场垂直导轨平面斜向上.有一质量为m的导体棒ab与导轨垂直放置,接触面粗糙且始终接触良好,导体棒的有效电阻也为R.现让导体棒从静止释放沿导轨下滑,当导体棒运动达到稳定状态时速率为v,此时整个电路消耗的电功率为重力功率的$\frac{3}{4}$.已知当地的重力加速度为g,导轨电阻不计.试求:
如图所示,足够长的平行金属导轨MN、PQ平行放置,间距为L,与水平面成θ角,导轨与固定电阻R1和R2相连,且R1=R2=R.R1支路串联开关S,原来S闭合,匀强磁场垂直导轨平面斜向上.有一质量为m的导体棒ab与导轨垂直放置,接触面粗糙且始终接触良好,导体棒的有效电阻也为R.现让导体棒从静止释放沿导轨下滑,当导体棒运动达到稳定状态时速率为v,此时整个电路消耗的电功率为重力功率的$\frac{3}{4}$.已知当地的重力加速度为g,导轨电阻不计.试求: