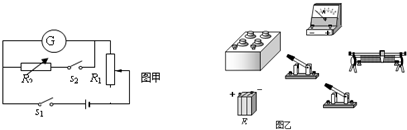
题目内容
6.如图所示,粒子源S可以不断地产生质量为m、电荷量为+q的粒子.粒子从O1孔飘进(不计初速度)一水平方向的加速度电场区域I,再经小孔O2进入正交的匀强电场和匀强磁场区域Ⅱ,电场强度大小为E,磁感应强度大小B1,方向如图.两平行虚线PQ、MN之间存在着水平向右的匀强磁场区域Ⅲ,磁场应强度大小为B2.当在O1、O2间加上适当的电压U1时,粒子能沿图中虚线O2O3垂直于PQ进入区域Ⅲ,并从MN边飞出.现将一块不带电的、宽度和厚度均不计的直角状硬质塑料板abc放置在区域Ⅲ内,a、c两点恰分别位于PQ、MN上,ac连线与O2O3平行,ab=bc=L,α=45°,仍使粒子沿图中虚线O2O3进入区域Ⅲ,发现粒子仍能从MN边飞出.粒子的重力不计.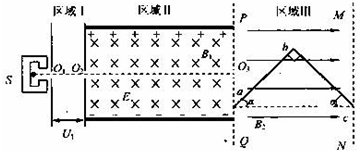
(1)求加速电压U1;
(2)假设粒子与硬质塑料板相碰后,速度大小不变,方向变化遵守光的反射定律,求粒子在区域Ⅲ中运动时,由于塑料板的放入而延迟的从MN边飞出的时间;
(3)粒子在区域Ⅲ内运动的总路程.
分析 (1)粒子源发出的粒子,进入加速电场被加速,由动能定理可以求出速度.粒子经过正交的电磁场时,电场力向下,洛伦兹力向上,都与速度垂直,合力为零,根据平衡条件列式求解加速电压U1;
(2)粒子进入PQ、MN之间的区域,由于速度方向与磁场方向平行,不受洛伦兹力而做匀速直线运动.粒子与ab板第一次碰撞后,速度向上,洛伦兹力提供向心力,在与ac边垂直的平面内做匀速圆周运动,经过一圈后,与ab边内侧碰撞,碰撞后水平向右运动,与bc边二次碰撞后,在与ac边垂直的平面内做再次匀速圆周运动,又经过一圈后,与b边外侧碰撞,水平向右离开磁场.根据运动轨迹,分匀速直线运动和匀速圆周运动求时间.对于匀速圆周运动,先计算半径和周期,再根据轨迹计算总时间,从而得到延迟的时间.
(3)根据洛伦兹力提供向心力,求出粒子在区域Ⅲ中运动的轨迹半径,由几何知识求路程.
解答 解(1)粒子从O1到O2,由动能定理得:
qU1=$\frac{1}{2}$mv02-0,
粒子从O2到O3做匀速直线运动,电场力与洛伦兹力平衡,则有 qE=qv0B1,
联立解得:U1=$\frac{m{E}^{2}}{2q{B}_{1}^{2}}$
(2)区域Ⅲ内无塑料板时,粒子不受洛伦兹力而做匀速直线运动,通过区域Ⅲ的时间为 t1=$\frac{2Lsin45°}{{v}_{0}}$;
区域Ⅲ内放入塑料板后,粒子从O3以速度v0进入区域III,先做匀速直线运动,打到ab板上,反弹后以速度v0垂直于磁场B2方向运动.粒子将以半径R在垂直于磁场的平面内作匀速圆周运动,转动一周后打到ab板的下部.由于不计板的厚度,所以粒子从第一次打到ab板到第二次打到ab板后运动的时间为粒子在磁场运动一周的时间,即一个周期T.粒子在磁场中共碰到2块板,做圆周运动所需的时间为t1=2T,有:
qvB2=m$\frac{{v}_{0}^{2}}{R}$
周期:T=$\frac{2πR}{{v}_{0}}$
粒子在磁场中做圆周运动所用的时间为:t2=2T
粒子在磁场中沿v0方向运动的时间为:t3=$\frac{2Lsin45°}{{v}_{0}}$
所以,由于塑料板的存在而延尺的时间为:$△t={t_2}+{t_3}-{t_1}=\frac{4πm}{{q{B_2}}}$
(3)因为 qvB2=m$\frac{{v}_{0}^{2}}{R}$
粒子在B2中的运动半径 $R=\frac{{m{v_0}}}{Bq}$
由几何关系可得,粒子在区域Ⅲ内运动的路程为:s=4πR+2Lsin45°
解得:s=$\sqrt{2}$L+$\frac{4πmE}{q{B}_{1}{B}_{2}}$
答:
(1)加速电压U1为$\frac{m{E}^{2}}{2q{B}_{1}^{2}}$.
(2)粒子在区域Ⅲ中运动时,由于塑料板的放入而延迟的从MN边飞出的时间为$\frac{4πm}{q{B}_{2}}$;
(3)粒子在区域Ⅲ内运动的总路程为$\sqrt{2}$L+$\frac{4πmE}{q{B}_{1}{B}_{2}}$.
点评 本题中的复合场具有速度选择的功能,进入磁场区域后,根据动力学规律先确定运动轨迹,再进行计算.

 阅读快车系列答案
阅读快车系列答案| A. | 万有引力定律是卡文迪许发现的 | |
| B. | 万有引力定律适用于自然界中的任何两个物体之间 | |
| C. | 万有引力定律公式F=$\frac{G{m}_{1}{m}_{2}}{{r}^{2}}$中的G是一个比例常数,是没有单位的 | |
| D. | 万有引力定律公式表明当r等于零时,万有引力为无穷大 |
| A. | 真空中a光的波长一定小于b光的波长 | |
| B. | a光能发生偏振现象,b光不能 | |
| C. | a光通过某障碍物能发生明显衍射现象,b光也一定能发生明显衍射 | |
| D. | 从某介质以相同的入射角射入空气时若a光能发生全反射,b光也一定能发生全反射 |
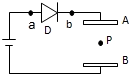 如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a.平行板电容器AB内部原有带电微粒P处于静止状态,当两极板A和B的间距稍增大一些后,微粒P的运动情况将是( )
如图所示,D是一只二极管,它的作用是只允许电流从a流向b,不允许电流从b流向a.平行板电容器AB内部原有带电微粒P处于静止状态,当两极板A和B的间距稍增大一些后,微粒P的运动情况将是( )| A. | 向上运动 | B. | 向下运动 | C. | 仍静止不动 | D. | 无法判断 |
| A. | 4:1 | B. | 9:4 | C. | 3:2 | D. | 16:9 |
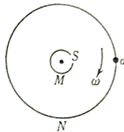 如图是德国物理学家史特恩设计的最早测定气体分子速率的示意图:M、N是两个共轴圆筒,外筒半径为R,内筒半径很小可忽略,筒的两段封闭,两筒之间抽成真空,两筒以相同角速度ω绕O匀速转动,M 筒开有与转轴平行的狭缝S,且不断沿半径方向向外射出速率为v1和v2的分子,分子到达N筒后被吸附,如果R、v1、v2保持不变,ω取一合适值,则( )
如图是德国物理学家史特恩设计的最早测定气体分子速率的示意图:M、N是两个共轴圆筒,外筒半径为R,内筒半径很小可忽略,筒的两段封闭,两筒之间抽成真空,两筒以相同角速度ω绕O匀速转动,M 筒开有与转轴平行的狭缝S,且不断沿半径方向向外射出速率为v1和v2的分子,分子到达N筒后被吸附,如果R、v1、v2保持不变,ω取一合适值,则( )| A. | 当|$\frac{R}{{v}_{1}}-\frac{R}{{v}_{2}}$|=n$\frac{2π}{ω}$时,分子落在同一狭条上(n取正整数) | |
| B. | 当$\frac{R}{{v}_{1}}+2\frac{R}{{v}_{2}}=n\frac{2π}{ω}$时,分子落在同一个狭条上(n取正整数) | |
| C. | 只要时间足够长,N筒上到处都落有分子 | |
| D. | 分子不可能落在N筒上某两处且与S平行的狭条上 |