题目内容
7．
如图所示，小球在竖直放置的光滑圆形管道内做圆周运动，内侧壁半径为R，小球半径为r，则下列说法正确的是（ ）| A． | 小球通过最高点时最小速度vmin=$\sqrt{g（R+r）}$ | |
| B． | 小球通过最高点时最小速度vmin=0 | |
| C． | 小球在水平线ab以下的管道中运动时，内侧管壁对小球可能有作用力 | |
| D． | 小球在水平线ab以上的管道中运动时，外侧管壁对小球一定有作用力 |
分析 小球在竖直光滑圆形管道内做圆周运动，在最高点，由于外管或内管都可以对小球产生弹力作用，从而可以确定在最高点的最小速度．小球做圆周运动是，沿半径方向的合力提供做圆周运动的向心力．根据牛顿第二定律求解管道对小球作用力大小和方向．
解答 解：A、B、由于管子能支撑小球，所以小球能够通过最高点时的最小速度为vmin=0；故A错误，B正确．
C、小球在水平线ab以下的管道中运动时，小球受到的合外力一部分是小球有竖直向下的加速度，另一部分使小球有直线圆心的向心加速度，所以小球受到的合力中，一部分是竖直向下的，该部分由重力提供；而另一部分直线圆心，则只能由外侧的管壁提供，所以内侧管壁对小球一定无作用力，而外侧管壁对小球一定有作用力．故C错误；
D、若小球的速度比较小，如小球恰好过最高点时，仅仅受到重力和内侧管壁的支持力，外侧管壁对小球没有作用力．故D错误．
故选：B．
点评 本题关键是对小球受力分析，然后根据牛顿第二定律和向心力公式列式求解．基础题目．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
18．甲、乙两物体都做匀速圆周运动，其质量之比为2：1，转动半径之比为2：1，在相等时间里甲转过45°，乙转过60°，则它们所受外力的合力之比为（ ）
| A． | 4：1 | B． | 9：4 | C． | 3：2 | D． | 16：9 |
2．一电饭煲和一台洗衣机同时并入u=311sin314tV的交流电源上，均正常工作，用电流表分别测得电饭煲的电流是5A，洗衣机的电流是0.5A．下列说法正确的是（ ）
| A． | 电饭煲的电阻是44Ω，洗衣机电动机线圈电阻是440Ω | |
| B． | 电饭煲消耗的功率为1 555 W，洗衣机电动机消耗的功率为155.5 W | |
| C． | 1 min内电饭煲消耗的电能为6.6×104 J，洗衣机电动机消耗的电能为6.6×103 J | |
| D． | 电饭煲的发热功率是洗衣机电动机发热功率的10倍 |
19．
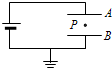如图所示，一带电油滴悬浮在平行板电容器两极板A、B之间的P点，处于静止状态．现将极板A向下平移一小段距离，但仍在P点上方，其它条件不变．下列说法中正确的是（ ）
如图所示，一带电油滴悬浮在平行板电容器两极板A、B之间的P点，处于静止状态．现将极板A向下平移一小段距离，但仍在P点上方，其它条件不变．下列说法中正确的是（ ）| A． | 液滴将向下运动 | B． | 液滴不动 | ||
| C． | 极板带电荷量将增加 | D． | 极板带电荷量将减少 |
16．
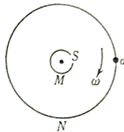如图是德国物理学家史特恩设计的最早测定气体分子速率的示意图：M、N是两个共轴圆筒，外筒半径为R，内筒半径很小可忽略，筒的两段封闭，两筒之间抽成真空，两筒以相同角速度ω绕O匀速转动，M 筒开有与转轴平行的狭缝S，且不断沿半径方向向外射出速率为v1和v2的分子，分子到达N筒后被吸附，如果R、v1、v2保持不变，ω取一合适值，则（ ）
如图是德国物理学家史特恩设计的最早测定气体分子速率的示意图：M、N是两个共轴圆筒，外筒半径为R，内筒半径很小可忽略，筒的两段封闭，两筒之间抽成真空，两筒以相同角速度ω绕O匀速转动，M 筒开有与转轴平行的狭缝S，且不断沿半径方向向外射出速率为v1和v2的分子，分子到达N筒后被吸附，如果R、v1、v2保持不变，ω取一合适值，则（ ）| A． | 当|$\frac{R}{{v}_{1}}-\frac{R}{{v}_{2}}$|=n$\frac{2π}{ω}$时，分子落在同一狭条上（n取正整数） | |
| B． | 当$\frac{R}{{v}_{1}}+2\frac{R}{{v}_{2}}=n\frac{2π}{ω}$时，分子落在同一个狭条上（n取正整数） | |
| C． | 只要时间足够长，N筒上到处都落有分子 | |
| D． | 分子不可能落在N筒上某两处且与S平行的狭条上 |
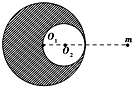如图所示为一质量为M的球形物体，密度均匀，半径为R，在距球心为2R处有一质量为m的质点，若将球体挖去一个半径为$\frac{R}{2}$的小球（两球心和质点在同一直线上，且挖去的球的球心在原来球心和质点连线之间，两球表面相切），则：