题目内容
A.质量为M的金属块和质量为m的木块用细线系在一起,以速度v在水中匀速下沉,某一时刻细线断了,在木块停止下沉前,金属块和木块组成的系统总动量 填m“守恒”或“不守恒”),当木块停止下沉的时刻,金属块下沉的速率为 .(设水足够深,水的阻力不计)
B、宇宙中有一种双星,质量分别为 m1,m2的两颗星球,绕同一圆心做匀速圆周运动,它们之间的距离恒为L,不考虑其他星体的影响,两颗星的轨道半径之比r1:r2是 ,周期是 .(万有引力恒量为G)
B、宇宙中有一种双星,质量分别为 m1,m2的两颗星球,绕同一圆心做匀速圆周运动,它们之间的距离恒为L,不考虑其他星体的影响,两颗星的轨道半径之比r1:r2是
分析:(1)木块和铁块用线系在一起,以速度v0在水中匀速下沉,说明它们的重力和与浮力大小相等,方向相反,合力为零,系统满足动量守恒定律,列出等式求解.
(2)双星以两者连线上某点为圆心,各自做匀速圆周运动,向心力由对方的万有引力提供,而且双星的条件是角速度相同,根据牛顿第二定律隔离两个天体分别研究,再求解星体m1的轨道半径和周期.
(2)双星以两者连线上某点为圆心,各自做匀速圆周运动,向心力由对方的万有引力提供,而且双星的条件是角速度相同,根据牛顿第二定律隔离两个天体分别研究,再求解星体m1的轨道半径和周期.
解答:解:A、木块和铁块以速度v0在水中匀速下沉,合力为零,木块和铁块组成系统满足动量守恒定律,规定向下为正方向得:
(M+m)v=0+Mv′
解得:v′=
B、根据牛顿第二定律有:
对星体m1:G
=m1?
…①
对星体m2:G
=m2?
…②
又r1+r2=L
联立解得:
=
;T=2π
故答案为:A.守恒,
,B.
,2π
(M+m)v=0+Mv′
解得:v′=
| (M+m)v |
| M |
B、根据牛顿第二定律有:
对星体m1:G
| m1m2 |
| L2 |
| 4π2r1 |
| T2 |
对星体m2:G
| m1m2 |
| L2 |
| 4π2r2 |
| T2 |
又r1+r2=L
联立解得:
| r1 |
| r2 |
| m2 |
| m1 |
|
故答案为:A.守恒,
| (M+m)v |
| M |
| m2 |
| m1 |
|
点评:(1)中判定出系统内竖直方向两个物体组成的系统动量守恒是解题的关键,比使用牛顿运动定律和运动学公式简单.
(2)本题是双星问题,与卫星绕地球运动模型不同,两颗星都绕同一圆心做匀速圆周运动,关键抓住条件:周期相同.
(2)本题是双星问题,与卫星绕地球运动模型不同,两颗星都绕同一圆心做匀速圆周运动,关键抓住条件:周期相同.

练习册系列答案
相关题目
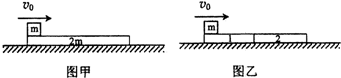 如图所示,将质量为2m、长度为L的木板静止地放在光滑水平面上,一质量为m的金属块(可视为质点),以水平初速度v0由木板左端恰能滑至木板的右端并与木板相对静止,金属块在运动过程中所受的摩擦力始终不变.现将木板分成长度与质量均相等的两段(1和2)后紧挨着放在此水平面上,让金属块仍以相同的初速度v0由木板的左端开始滑动,如图乙所示.
如图所示,将质量为2m、长度为L的木板静止地放在光滑水平面上,一质量为m的金属块(可视为质点),以水平初速度v0由木板左端恰能滑至木板的右端并与木板相对静止,金属块在运动过程中所受的摩擦力始终不变.现将木板分成长度与质量均相等的两段(1和2)后紧挨着放在此水平面上,让金属块仍以相同的初速度v0由木板的左端开始滑动,如图乙所示.