Question

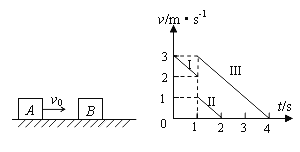
【题目】如图所示，光滑水平面上有一质量为m＝1kg的小车，小车右端固定一水平轻质弹簧，弹簧左端连接一质量为m0＝1kg的物块，物块与上表面光滑的小车一起以v0＝5m/s的速度向右匀速运动，与静止在光滑水平面上、质量为M＝4kg的小球发生弹性正碰，若碰撞时间极短，弹簧始终在弹性限度内．则（ ）

A. 碰撞结束时，小车的速度为3m/s，速度方向向左

B. 从碰后瞬间到弹簧最短的过程，弹簧弹力对小车的冲量大小为4N·s

C. 小车的最小速度为1m/s

D. 在小车速度为1m/s时，弹簧的弹性势能有最大值

Answer 1

【答案】ABD

【解析】

A、设碰撞后瞬间小车的速度大小为v1，小球的速度大小为v，由动量守恒及动能守恒有：

mv0＝Mv＋mv1，；解得：，小车速度方向向左；，小球速度方向向右；选项A正确。

D、当弹簧被压缩到最短时，设小车的速度大小为v2，根据动量守恒定律有：m0v0＋mv1＝(m0＋m)v2，解得：v2＝1 m/s，选项D正确。

C、由以上分析可知小车最小速度为0，选项C错误。

B、设从碰撞的瞬间到弹簧最短的过程，弹簧弹力对小车的冲量大小为I，根据动量定理有I＝mv2－mv1，解得：I＝4N·s，选项B正确。

故选ABD。