Question

【题目】某三棱镜的横截面为一直角三角形，如图所示，∠A＝90°，∠B＝30°，∠C＝60°，棱镜材料的折射率为n，底面BC涂黑，入射光沿平行与底面BC的方向射向AB面，经AB面和AC面折射后出射。

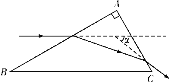
①求出射光线和入射光线延长线的夹角α；（可用反三角函数表示角度）

②为使上述入射光线能从AC面出射，折射率n的最大值为多少？

Answer 1

【答案】（1） （2）

【解析】

①完成光路图，根据折射定律求出光线在AB面上折射角，由几何知识求出光线射到AC面上的入射角，再由折射定律求出AC面上的折射角，即可由几何关系求出出射光线和入射光线延长线的夹角δ．

②入射光线能从AC面出射时，光线不能在AC面上发生全反射，折射角的正弦值不大于1，由此求折射率n的最大值．

画出光路图如图所示：

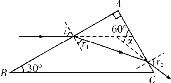
.①因为入射光平行于BC面，可得i＝60°，由 ＝n

得sin r1＝

又 ，则得sin r2＝ncos r1＝

故α＝60°－(90°－r2)＝arcsin－30°

②要使光线从AC面射出，应有sin r2≤1，即有 ≤1，

解之得n≤

所以n的最大值为。