题目内容
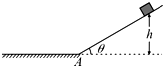
【题目】如图,半径R=0.8m的光滑圆弧轨道固定在水平地面上,O为该圆弧的圆心,轨道上方的A处有一个可视为质点的质量m=1kg的小物块,小物块由静止开始下落后恰好沿切线进入圆弧轨道.此后小物块将沿圆弧轨道下滑,已知AO连线与水平方向的夹角θ=45°,在轨道末端C点紧靠一质量M=3kg的长木板,木板上表面与圆弧轨道末端的切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,g取10m/s2 . 求: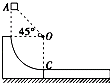
(1)小物块刚到达C点时的速度大小;
(2)小物块刚要到达圆弧轨道末端C点时对轨道的压力;
(3)要使小物块不滑出长木板,木板长度L至少为多少?
【答案】
(1)解:小物块从A到C,机械能守恒,设在C点的速度为vC
因为 ![]()
所以 ![]()
故小物块刚到达C点时的速度大小为 ![]()
(2)解:对小物块,在C点受到重力和轨道对它的竖直向上的支持力.由牛顿第二定律得:
![]()
则 ![]()
= ![]()
=50N
由牛顿第三定律得:小物块刚要到达圆弧轨道末端C点时对轨道的压力的大小为50N,方向竖直向下.
故小物块刚要到达圆弧轨道末端C点时对轨道的压力的大小为50N,方向竖直向下.
(3)解:对小物块,在C点受到重力和轨道对它的竖直向上的支持力.由牛顿第二定律得:
![]()
则 ![]()
= ![]()
=50N
由牛顿第三定律得:小物块刚要到达圆弧轨道末端C点时对轨道的压力的大小为50N,方向竖直向下.
故小物块刚要到达圆弧轨道末端C点时对轨道的压力的大小为50N,方向竖直向下.
设小物块刚滑到木板右端时达到共同速度,大小为v
对系统,由动量守恒定律得:
mvc=(M+m)v
则 ![]()
= ![]()
= ![]()
对小物块,与长木板发生相对滑动的过程中,由动能定理得:
![]()
带人数据解得:小物块在该过程中相对于地面所发生的位移 xm=5m
对长木板,与小物块发生相对滑动的过程中,由动能定理得:
![]()
带人数据解得:长木板在该过程中相对于地面所发生的位移xM=1m
长木板的长度至少为L=xm﹣xM
=5m﹣1m
=4m
答:要使小物块不滑出长木板,木板长度L至少为4 m.
【解析】(1)物体下滑到c的过程中,机械能守恒,利用机械能守恒定律列式求解。
(2)物体滑到c点时所受的合外力,提供向心力,结合向心力公式,以及受力分析,求解即可。
(3)物化而不滑出长木板代表物块滑到长木板右端时,应与长木板速度相同,分析整个过程,利用动量守恒和动能定理列方程求解。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案