��Ŀ����
2��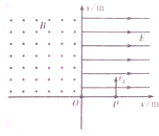 ��ͼ��ʾ����xoyƽ���ڵĵ�һ�����ڴ��ڵ糡ǿ��ΪE=2V/m����x�����������ǿ�糡���ڵڶ������ڴ��ڴŸ�Ӧǿ��B=1T������ֱxoyƽ���������ǿ�ų���һ������������ӣ��Ⱥ�Ϊ4C/kg����x=3m����P����v0=4m/s�ij��ٶ���y��������ʼ�˶������ƴ������ӵ���������
��ͼ��ʾ����xoyƽ���ڵĵ�һ�����ڴ��ڵ糡ǿ��ΪE=2V/m����x�����������ǿ�糡���ڵڶ������ڴ��ڴŸ�Ӧǿ��B=1T������ֱxoyƽ���������ǿ�ų���һ������������ӣ��Ⱥ�Ϊ4C/kg����x=3m����P����v0=4m/s�ij��ٶ���y��������ʼ�˶������ƴ������ӵ�����������1���������ӵ�һ��ͨ��y��ʱ��O��ľ��룮
��2�����������ٴ�ͨ��x��ʱ��O��ľ��룮
���� ��1�������ڵ�һ����������ƽ���˶����ص糡�ߵķ��������ȼ���ֱ���˶�������ƽ���˶�֪ʶ����������ӵ�һ��ͨ��y��ʱ��O��ľ��룮
��2�������ڴų���������Բ���˶��������������ṩ�������ó������˶��İ뾶��Ȼ���ϼ���֪ʶ������������ٴ�ͨ��x��ʱ��O��ľ��룮
��� �⣺��1���糡�߷����У�qE=ma
�ã�$a=\frac{qE}{m}=4��2=8m/{s}^{2}$
��$x=\frac{1}{2}a{t}^{2}$�ã�$t=\sqrt{\frac{2x}{a}}=\sqrt{\frac{2��3}{8}}=\frac{\sqrt{3}}{2}$s
y�᷽���У�y=v0t
�������ݽ�ã�$y=2\sqrt{3}$m
��2���ɣ�1����֪���ӽ���ų�ʱ��
${v}_{x}=at=8��\frac{\sqrt{3}}{2}=4\sqrt{3}$m/s
vx��v0����нǣ�$tan��=\frac{{v}_{y}}{{v}_{x}}=\frac{4\sqrt{3}}{4}=\sqrt{3}$
����=60��
${v}_{t}=\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}=8$m/s
���������ڴų���������Բ���˶��İ뾶��r=$\frac{mv}{qB}$=$\frac{8}{2��2}=2$m
�ɼ���֪ʶ��֪MNΪԲ���˶���ֱ����NO=r=2m
�𣺣�1���������ӵ�һ��ͨ��y��ʱ��O��ľ�����$2\sqrt{3}$m����2�����������ٴ�ͨ��x��ʱ��O��ľ�����2m��
���� ���⿼���˴��������ڵ糡��ų��е��˶������������ڵ糡������ƽ���˶����ڴų���������Բ���˶�����������������˶����̣�Ӧ����ƽ���˶�������ţ�ٵڶ����ɼ�����ȷ����

 �ס������������������һ������ͬʱ�شֲڵĹ̶�б�������»�����������б���Ķ�Ħ��������ͬ����m����m���������ܵ�����Ϊ��������
�ס������������������һ������ͬʱ�شֲڵĹ̶�б�������»�����������б���Ķ�Ħ��������ͬ����m����m���������ܵ�����Ϊ���������������ڼ��ҵĵ�����б����ҵĵ�����б����ҵ�Ħ������
| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �٢ۢ� | D�� | �٢ڢۢ� |
| A�� | ̫������������Ҫ����̫���ڲ��ĺ˾۱䷴Ӧ | |
| B�� | һ����ɫ�����䵽ij�ֽ������治�ܷ������ЧӦ������Ϊ�ù�IJ���̫�� | |
| C�� | �������ЧӦʱ��������Ƶ��Խ�ߣ��ݳ��Ĺ���ӵ��������ܾ�Խ�� | |
| D�� | ��������ԭ�Ӵ�n=3�ܼ�����ܼ�ԾǨʱ��ֻ�ܷ������ֲ�ͬƵ�ʵĹ� | |
| E�� | ԭ�Ӻ˷���һ�Φ�˥�䣬�ͻ�����һ������ |
| A�� | $\frac{p}{q}$v | B�� | $\frac{q}{p}$v | C�� | $\sqrt{\frac{p}{q}}$v | D�� | $\sqrt{\frac{q}{p}}$v |
| A�� | �Ա�ڿռ�վ�ڴ���Ư��״̬���������Dz������� | |
| B�� | ������׳ߴӵ����ϴ�����ת���ʱȵ�����ij�����ϣ����׳ߵij���һ������ | |
| C�� | ���϶�һ�š��������Ǿ�����챻�������������پ���α�죬����������������Բ���˶�������������������������a��������뾶������뾶b�����������Ƶ���������渽����Բ���˶�������֮��Ϊ$\sqrt{ab}$ | |
| D�� | ��֪��������������������81�������������ļ�ľ���ΪL�������϶�һ�š����������ڵ������������ܺ���Ϊ�㴦����������������˴������ĵľ���Ϊ0.9L |
 ��ͼ��ʾ���⻬��ˮƽ��������һľ�壬����˷���һ����ҷ���һ��ֱ��ǽ�ڣ���������Ϊľ��������������������ľ���Ķ�Ħ������Ϊ?��ʹľ���������Թ�ͬ���ٶ�v0�����˶���ijʱ��ľ����ǽ����������ײ����ײʱ�伫�̣���ľ��ӵ�һ����ǽ����ײ���ٴ��������ٶ���ͬʱ��ľ���Ҷ���ǽ�ڵľ��룮
��ͼ��ʾ���⻬��ˮƽ��������һľ�壬����˷���һ����ҷ���һ��ֱ��ǽ�ڣ���������Ϊľ��������������������ľ���Ķ�Ħ������Ϊ?��ʹľ���������Թ�ͬ���ٶ�v0�����˶���ijʱ��ľ����ǽ����������ײ����ײʱ�伫�̣���ľ��ӵ�һ����ǽ����ײ���ٴ��������ٶ���ͬʱ��ľ���Ҷ���ǽ�ڵľ��룮 ��ͼ��ʾ��ֱ��������ABC��һ����ש�ĺ���棬AB=L����C=90�㣬��A=60�㣮һ����ɫ��PD��AB���ϵ�D�����벣��ש�������Ϊ45�㣬DB=$\frac{L}{4}$�������DEǡ���䵽����שBC�ߵ��е�E����֪��������еĴ����ٶ�Ϊc����
��ͼ��ʾ��ֱ��������ABC��һ����ש�ĺ���棬AB=L����C=90�㣬��A=60�㣮һ����ɫ��PD��AB���ϵ�D�����벣��ש�������Ϊ45�㣬DB=$\frac{L}{4}$�������DEǡ���䵽����שBC�ߵ��е�E����֪��������еĴ����ٶ�Ϊc���� ��ͼ��ʾ������ϵxOy����ֱƽ���ڣ�x����ˮƽ���ڶ������д�ֱ����ƽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB1=$\sqrt{\frac{18{E}^{2}}{5��•gL}}$����������ͬʱ�����Ŵ�ֱ������ƽ���������ǿ�ų�����ֱ���µ���ǿ�糡���Ÿ�Ӧǿ�ȴ�СΪB2=$\sqrt{\frac{5��{E}^{2}}{6gL}}$���糡ǿ��ΪE����Сδ֪�����ڵڶ������ڹ̶�һ����x��ɦ�=30��ǵľ�Եϸ�ˣ�һ������С��a����ϸ���������»�ͨ��O�����������ޣ��ڵ���������������Բ���˶��Ҿ���x���ϵ�O�㣬��֪Q�㵽����ԭ��O�ľ���ΪL���������ٶ�Ϊg�������������Բ��ƣ���
��ͼ��ʾ������ϵxOy����ֱƽ���ڣ�x����ˮƽ���ڶ������д�ֱ����ƽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB1=$\sqrt{\frac{18{E}^{2}}{5��•gL}}$����������ͬʱ�����Ŵ�ֱ������ƽ���������ǿ�ų�����ֱ���µ���ǿ�糡���Ÿ�Ӧǿ�ȴ�СΪB2=$\sqrt{\frac{5��{E}^{2}}{6gL}}$���糡ǿ��ΪE����Сδ֪�����ڵڶ������ڹ̶�һ����x��ɦ�=30��ǵľ�Եϸ�ˣ�һ������С��a����ϸ���������»�ͨ��O�����������ޣ��ڵ���������������Բ���˶��Ҿ���x���ϵ�O�㣬��֪Q�㵽����ԭ��O�ľ���ΪL���������ٶ�Ϊg�������������Բ��ƣ���