题目内容
10. 如图所示,直角三角形ABC是一玻璃砖的横截面,AB=L,∠C=90°,∠A=60°.一束单色光PD从AB边上的D点射入玻璃砖,入射角为45°,DB=$\frac{L}{4}$,折射光DE恰好射到玻璃砖BC边的中点E,已知光在真空中的传播速度为c.求:
如图所示,直角三角形ABC是一玻璃砖的横截面,AB=L,∠C=90°,∠A=60°.一束单色光PD从AB边上的D点射入玻璃砖,入射角为45°,DB=$\frac{L}{4}$,折射光DE恰好射到玻璃砖BC边的中点E,已知光在真空中的传播速度为c.求:(ⅰ)玻璃砖的折射率;
(ⅱ)该光束从AB边上的D点射入玻璃砖到第一次射出玻璃砖所需的时间.
分析 (i)先据题意作出光路图,由几何知识求出光在AB边折射时的折射角,即可求得折射率.
(ii)设临界角为θ,由sinθ=$\frac{1}{n}$,求出临界角θ,可判断出光在BC边上发生了全反射,在AC边第一次射出玻璃砖,由光路图及几何知识求出光束从AB边射入玻璃砖到第一次射出玻璃砖通过的路程,由公式v=$\frac{c}{n}$求光在玻璃中的传播速度,即可求得时间.
解答  解:(ⅰ)作出光路图,如图所示
解:(ⅰ)作出光路图,如图所示
过E点的法线是三角形的中位线,由几何关系可知△DEB为等腰三角形,DE=DB=$\frac{L}{4}$
由几何知识可知光在AB边折射时折射角为 r=30°,
所以玻璃砖的折射率为 n=$\frac{sini}{sinr}$=$\frac{sin45°}{sin30°}$=$\sqrt{2}$
(ⅱ)设临界角为θ,有sinθ=$\frac{1}{n}$,可解得 θ=45°
由光路图及几何知识可判断,光在BC边上的入射角为60°,大于临界角,则光在BC边上发生全反射
光在AC边的入射角为30°,小于临界角,所以光从AC第一次射出玻璃砖
根据几何知识可知 EF=$\frac{L}{2}$
则光束从AB边射入玻璃砖到第一次射出玻璃砖所需要的时间为
t=$\frac{DE+EF}{v}$
而v=$\frac{c}{n}$,可解得:t=$\frac{3\sqrt{2}L}{4c}$
答:
(ⅰ)玻璃砖的折射率为$\sqrt{2}$;
(ⅱ)该光束从AB边上的D点射入玻璃砖到第一次射出玻璃砖所需的时间为$\frac{3\sqrt{2}L}{4c}$.
点评 解决本题关键是作出光路图,再运用几何知识求解入射角折射角,要掌握几何光学常用的三个规律:折射定律n=$\frac{sini}{sinr}$、临界角公式sinC=$\frac{1}{n}$和光速公式v=$\frac{c}{n}$.

| A. | 同学处于失重状态,体重计的读数小于同学的体重 | |
| B. | 同学处于失重状态,体重计的读数大于同学的体重 | |
| C. | 同学先失重再超重,体重计的读数先小于同学的体重再大于同学的体重 | |
| D. | 同学先超重再失重,体重计的读数先大于同学的体重再小于同学的体重 |

| A. | 电压表的读数为448V | |
| B. | 输电线路的电流为0.98A | |
| C. | 电流表的读数为2.5A | |
| D. | 降压变压器的原副线圈匝数比为5:1 |
 如图所示,一根长为L=3m的竖直绳子末端挂着一个质量为m=1kg的木块(可视为质点),现给木块一个水平方向的初速度v0=4m/s,使木块开始摆动.当绳子摆到与竖直方向的夹角θ=37°时,绳突然断了,绳断后,木块恰能运动到水平传送带的最左端,且此时速度水平,此后木块在传迭带上滑行.已知传送带足够长,正以v′=1m/s的恒定速度逆时针运行,木块与传送带间的动摩擦因数μ=0.2,不考虑空气阻力和绳的质量,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.下列说法中正确的是( )
如图所示,一根长为L=3m的竖直绳子末端挂着一个质量为m=1kg的木块(可视为质点),现给木块一个水平方向的初速度v0=4m/s,使木块开始摆动.当绳子摆到与竖直方向的夹角θ=37°时,绳突然断了,绳断后,木块恰能运动到水平传送带的最左端,且此时速度水平,此后木块在传迭带上滑行.已知传送带足够长,正以v′=1m/s的恒定速度逆时针运行,木块与传送带间的动摩擦因数μ=0.2,不考虑空气阻力和绳的质量,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.下列说法中正确的是( )| A. | 绳断时木块的速度大小为2m/s | |
| B. | 木块刚好到达传送带最左端时的速度大小为1m/s | |
| C. | 木块在传送带上距传送带左端的最大距离是1.28m | |
| D. | 木块从滑上传送带到离开传送带的过程中,整个系统因摩擦而产生的热量为3.38J |
 如图所示,由一根金属导线绕成闭合线圈,线圈圆的半径分别为R、2R,磁感应强度B随时间t的变化规律是B=kt(k为常数),方向垂直于线圈平面.闭合线圈中产生的感应电动势为( )
如图所示,由一根金属导线绕成闭合线圈,线圈圆的半径分别为R、2R,磁感应强度B随时间t的变化规律是B=kt(k为常数),方向垂直于线圈平面.闭合线圈中产生的感应电动势为( )| A. | kπR2 | B. | 3kπR2 | C. | 4kπR2 | D. | 5kπR2 |
 在“探究力的平行四边形定则”的实验中,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.
在“探究力的平行四边形定则”的实验中,用图钉把橡皮条的一端固定在板上的A点,在橡皮条的另一端拴上两条细绳,细绳另一端系着绳套B、C(用来连接弹簧测力计).其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.
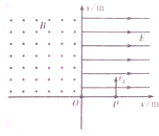 如图所示,在xoy平面内的第一象限内存在电场强度为E=2V/m,沿x轴正方向的匀强电场,在第二象限内存在磁感应强度B=1T、方向垂直xoy平面向外的匀强磁场,一个带负电的粒子,比荷为4C/kg,在x=3m处的P点以v0=4m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力,球:
如图所示,在xoy平面内的第一象限内存在电场强度为E=2V/m,沿x轴正方向的匀强电场,在第二象限内存在磁感应强度B=1T、方向垂直xoy平面向外的匀强磁场,一个带负电的粒子,比荷为4C/kg,在x=3m处的P点以v0=4m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力,球: 如图所示,在y>0的空间中存在匀强电场,电场方向沿y轴正方向;在y<0的空间中存在匀强磁场,磁场方向垂直平面(纸面)向里,一电荷量为q、质量为m的带负电的运动粒子,经过y轴上y=h处的点P1时速度大小为v0,方向沿x轴正方向;然后经过x轴上x=2h处的P2点进入磁场,再经x=-2h的P3点再次进入电场.粒子重力不计.求:
如图所示,在y>0的空间中存在匀强电场,电场方向沿y轴正方向;在y<0的空间中存在匀强磁场,磁场方向垂直平面(纸面)向里,一电荷量为q、质量为m的带负电的运动粒子,经过y轴上y=h处的点P1时速度大小为v0,方向沿x轴正方向;然后经过x轴上x=2h处的P2点进入磁场,再经x=-2h的P3点再次进入电场.粒子重力不计.求: