Question

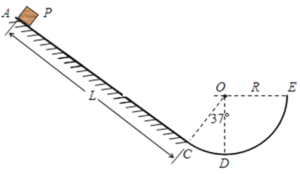
【题目】如图所示，粗糙斜面ABC下端与光滑的圆弧轨道CDE相切于C，整个装置竖直固定，D是最低点，圆心角∠DOC=37°，E与圆心O等高，圆弧轨道半径R=0.5m，斜面长L=2m，现有一个质量m=0.10kg的小物块P从斜面上端A点无初速下滑，物块P与斜面AC间的动摩擦因数。取sin37°=0.6，cos37°=0.8，重力加速度g=10m/s2，忽略空气阻力。求：

(1)物块第一次通过C点时的速度大小vC；

(2)物块第一次通过D点后在右侧轨道上所能上升的最大高度；

(3)物块在AC上滑行的总路程s。

Answer 1

【答案】(1)；(2)0.5m；(3)3m

【解析】

(1)物块在AC段运动的过程中应用动能定理得

解得

(2)物块在圆弧上滑动时，由动能定理

解得

h=0.5m

(3)滑块在斜面和圆弧上来回运动，在斜面上的高度逐渐降低，最终将在圆弧上以C为最高点来回滚动，则由能量关系

解得

s=3m