题目内容
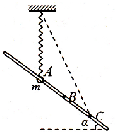
4．
如图，支架固定在水平地面上，其倾斜的光滑直杆与地面成30°角，两圆环A、B穿在直杆上，并用跨过光滑定滑轮的轻绳连接，滑轮的大小不计，整个装置处于同一竖直平面内．圆环平衡时，绳OA竖直，绳OB与直杆间夹角为30°．则环A、B的质量之比为（ ）| A． | 1：$\sqrt{3}$ | B． | 1：2 | C． | $\sqrt{3}$：1 | D． | $\sqrt{3}$：2 |
分析 分别对AB两球分析，运用合成法，分别用T表示出A、B两球的重力，同一根绳子上的拉力相等，即绳子AB两球的拉力是相等的．
解答 解：分别对A、B两球分析，运用合成法，如图：
以A为研究对象，则A只能受到重力和绳子的拉力的作用，杆对A不能有力的作用，否则A水平方向受力不能平衡．所以：T=mAg
以B为研究对象，根据共点力平衡条件，结合图可知，绳子的拉力T与B受到的支持力N与竖直方向之间的夹角都是30°，所以T与N大小相等，得：
mBg=2×Tcos30°=$\sqrt{3}T$
故mA：mB=1：$\sqrt{3}$
故选：A
点评 本题考查了隔离法对两个物体的受力分析，关键是抓住同一根绳子上的拉力处处相等结合几何关系将两个小球的重力联系起来．
练习册系列答案
相关题目
14．如图所示，电容器上标有“400V 2.2μF”的字样，下列说法正确的是（ ）
| A． | 该电容器两端电压是400V时，电容为2.2μF | |
| B． | 该电容器的带电量是28.8×10-4C | |
| C． | 该电容器的工作电压是400V | |
| D． | 该电容器的击穿电压是400V |
15．一电荷从A点移到零势能位置时，静电力做功5J，则该电荷在A点电势能为（ ）
| A． | 0J | B． | -5J | C． | 2.5J | D． | 5J |
19．
空降兵某部官兵使用新装备进行超低空跳伞训练．若跳伞空降兵在离地面224m高处由静止开始在竖直方向做自由落体运动．-段时间后立即打开降落伞，以12.5m/s2的平均加速度匀减速下降．为了空降兵的安全，要求空降兵落地速度最大不得超过5m/s（g取10m/s2）．则（ ）
空降兵某部官兵使用新装备进行超低空跳伞训练．若跳伞空降兵在离地面224m高处由静止开始在竖直方向做自由落体运动．-段时间后立即打开降落伞，以12.5m/s2的平均加速度匀减速下降．为了空降兵的安全，要求空降兵落地速度最大不得超过5m/s（g取10m/s2）．则（ ）| A． | 空降兵展开伞时离地面高度至少为125m | |
| B． | 空降兵展开伞时离地面高度至少为99m | |
| C． | 空降兵落地落地相当于从1.25m高处自由落下 | |
| D． | 空降兵落地落地相当于从2.5m高处自由落下 |
9．
如图所示，轻质弹簧一端固定，另一端与质量为m的圆环相连，圆环套在倾斜的粗糙固定杆上，杆与水平面之间的夹角为α，圆环在A处时弹簧竖直且处于原长．将圆环从A处静止释放，到达C处时速度为零．若圆环在C处获得沿杆向上的速度v，恰好能回到A．已知AC=L，B是AC的中点，弹簧始终在弹性限度之内，重力加速度为g，则（ ）
如图所示，轻质弹簧一端固定，另一端与质量为m的圆环相连，圆环套在倾斜的粗糙固定杆上，杆与水平面之间的夹角为α，圆环在A处时弹簧竖直且处于原长．将圆环从A处静止释放，到达C处时速度为零．若圆环在C处获得沿杆向上的速度v，恰好能回到A．已知AC=L，B是AC的中点，弹簧始终在弹性限度之内，重力加速度为g，则（ ）| A． | 下滑过程中，环受到的合力不断减小 | |
| B． | 下滑过程中，环与杆摩擦产生的热量为$\frac{1}{4}$mv2 | |
| C． | 从C到A过程，弹簧对环做功为mgLsinα-$\frac{1}{4}$mv2 | |
| D． | 环经过B时，上滑的速度大于下滑的速度 |
16．如图所示是某质点运动的速度图象，由图象得到的正确结果是（ ）
| A． | 0～1s内的平均速度是2m/s | |
| B． | 0～2s内的位移大小是3m | |
| C． | 0～1s内的加速度小于2～4s内的加速度 | |
| D． | 0～4s内物体平均速度0m/s |
氢气球重10N，所受空气浮力为16N，由于受到水平风力，使系氢气球的轻绳和水平地面成α=60°角而静止，如图所示．求：