题目内容
9.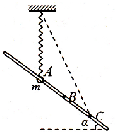 如图所示,轻质弹簧一端固定,另一端与质量为m的圆环相连,圆环套在倾斜的粗糙固定杆上,杆与水平面之间的夹角为α,圆环在A处时弹簧竖直且处于原长.将圆环从A处静止释放,到达C处时速度为零.若圆环在C处获得沿杆向上的速度v,恰好能回到A.已知AC=L,B是AC的中点,弹簧始终在弹性限度之内,重力加速度为g,则( )
如图所示,轻质弹簧一端固定,另一端与质量为m的圆环相连,圆环套在倾斜的粗糙固定杆上,杆与水平面之间的夹角为α,圆环在A处时弹簧竖直且处于原长.将圆环从A处静止释放,到达C处时速度为零.若圆环在C处获得沿杆向上的速度v,恰好能回到A.已知AC=L,B是AC的中点,弹簧始终在弹性限度之内,重力加速度为g,则( )| A. | 下滑过程中,环受到的合力不断减小 | |
| B. | 下滑过程中,环与杆摩擦产生的热量为$\frac{1}{4}$mv2 | |
| C. | 从C到A过程,弹簧对环做功为mgLsinα-$\frac{1}{4}$mv2 | |
| D. | 环经过B时,上滑的速度大于下滑的速度 |
分析 根据圆环的运动情况分析下滑过程中,加速度的变化;
研究圆环从A处由静止开始下滑到C和在C处获得一竖直向上的速度v,恰好能回到A两个过程,运用动能定理列出等式求解;
研究圆环从A处由静止开始下滑到B过程和圆环从B处上滑到A的过程,运用动能定理列出等式.
解答 解:A、圆环从A处由静止开始下滑,初速度为零,到达C处的速度为零,所以圆环先做加速运动,再做减速运动,所以加速度先减小,后增大,则合力先减小后增大,故A错误;
B、研究圆环从A处由静止开始下滑到C过程,运用动能定理列出等式
mgh+Wf-W弹=0-0=0
在C处获得一竖直向上的速度v,恰好能回到A,运用动能定理列出等式
-mgh+W弹+Wf=0-$\frac{1}{2}$mv2
解得:Wf=-$\frac{1}{4}$mv2,所以产生的热量为$\frac{1}{4}$mv2,故B正确;
C、在C处获得一竖直向上的速度v,恰好能回到A,运用动能定理列出等式
-mgh+W弹+Wf=0-$\frac{1}{2}$mv2,h=Lsinα,
解得:W弹=mgLsinα-$\frac{1}{4}$mv2,故C正确;
D、研究圆环从A处由静止开始下滑到B过程,运用动能定理列出等式
mgh′+W′f-W′弹=$\frac{1}{2}m{{v}_{B}}^{2}$-0
研究圆环从B处上滑到A的过程,运用动能定理列出等式
-mgh′+W′f+W′弹=0-$\frac{1}{2}m{{v}_{B}′}^{2}$
由于W′f<0,所以$\frac{1}{2}m{{v}_{B}}^{2}<\frac{1}{2}m{{v}_{B}′}^{2}$,则环经过B时,上滑的速度大于下滑的速度,故D正确;
故选:BCD
点评 能正确分析小球的受力情况和运动情况,对物理过程进行受力、运动、做功分析,是解决问题的根本方法,掌握动能定理的应用.

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案| A. | 7.9m/s | B. | 9.2m/s | C. | 7.8m/s | D. | 8.0m/s |
 如图,支架固定在水平地面上,其倾斜的光滑直杆与地面成30°角,两圆环A、B穿在直杆上,并用跨过光滑定滑轮的轻绳连接,滑轮的大小不计,整个装置处于同一竖直平面内.圆环平衡时,绳OA竖直,绳OB与直杆间夹角为30°.则环A、B的质量之比为( )
如图,支架固定在水平地面上,其倾斜的光滑直杆与地面成30°角,两圆环A、B穿在直杆上,并用跨过光滑定滑轮的轻绳连接,滑轮的大小不计,整个装置处于同一竖直平面内.圆环平衡时,绳OA竖直,绳OB与直杆间夹角为30°.则环A、B的质量之比为( )| A. | 1:$\sqrt{3}$ | B. | 1:2 | C. | $\sqrt{3}$:1 | D. | $\sqrt{3}$:2 |
| A. | 6m/s | B. | 6.25m/s | C. | 6.75m/s | D. | 7.0m/s |
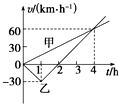 t=0时,甲乙两汽车从相距90km的两地开始相向行驶,它们的v-t图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( )
t=0时,甲乙两汽车从相距90km的两地开始相向行驶,它们的v-t图象如图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是( )| A. | 在第1小时末,乙车改变运动方向 | |
| B. | 在第2小时末,甲乙两车相距10 km | |
| C. | 在前4小时内,乙车运动加速度的大小总比甲车的大 | |
| D. | 在第4小时末,甲乙两车相遇 |
| A. | 研究火车在平直轨道上运行时车轮的转动 | |
| B. | 乒乓球比赛中,研究运动员发出的旋转球的运动 | |
| C. | 研究航天员翟志刚在太空出舱挥动国旗的动作 | |
| D. | 用GPS确定打击海盗的“武汉”舰在大海中的位置 |
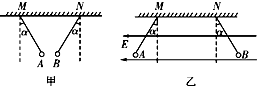 质量都是m的两个完全相同、带等量异种电荷的小球A、B分别用长l的绝缘细线悬挂在同一水平面上相距为2l的M、N两点,平衡时小球A、B的位置如图甲所示,线与竖直方向夹角θ=30°.当空间加沿MN方向的匀强电场时,两小球平衡时如图乙所示,线与竖直方向夹角也是θ=30°.重力加速度为g,静电力常量为k.求:
质量都是m的两个完全相同、带等量异种电荷的小球A、B分别用长l的绝缘细线悬挂在同一水平面上相距为2l的M、N两点,平衡时小球A、B的位置如图甲所示,线与竖直方向夹角θ=30°.当空间加沿MN方向的匀强电场时,两小球平衡时如图乙所示,线与竖直方向夹角也是θ=30°.重力加速度为g,静电力常量为k.求: 如图击剑比赛中,甲的剑击中乙的导电服,乙头顶上的指示灯就会亮;乙的剑击中甲的导电服,甲头顶上的指示灯就会亮.这里剑相当于“开关”,选项中能反映上述比赛原理的电路图是( )
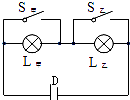
如图击剑比赛中,甲的剑击中乙的导电服,乙头顶上的指示灯就会亮;乙的剑击中甲的导电服,甲头顶上的指示灯就会亮.这里剑相当于“开关”,选项中能反映上述比赛原理的电路图是( )

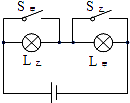
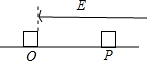 如图所示,在绝缘水平面上,O点右侧有一匀强电场,电场方向水平向左,一带正电的小滑块以速度v=0.6m/s从O点进入匀强电场,向右运动最远到达P点,O、P间的距离L=0.06m,小滑块的质量为m=1×10-3kg,带电量为q=2×10-5C,小滑块与水平面的动摩擦因数为0.1,设最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2,求:
如图所示,在绝缘水平面上,O点右侧有一匀强电场,电场方向水平向左,一带正电的小滑块以速度v=0.6m/s从O点进入匀强电场,向右运动最远到达P点,O、P间的距离L=0.06m,小滑块的质量为m=1×10-3kg,带电量为q=2×10-5C,小滑块与水平面的动摩擦因数为0.1,设最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2,求: