题目内容
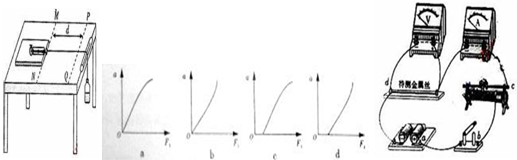
 (1)某同学设计了一个测量物体质量的装置,如图1所示,其中P是光滑水平轨道,A是质量为M的带夹子的已知质量金属块,Q是待测质量的物体(可以被A上的夹子固定).已知该装置的弹簧振子做简谐运动的周期为T=2π
(1)某同学设计了一个测量物体质量的装置,如图1所示,其中P是光滑水平轨道,A是质量为M的带夹子的已知质量金属块,Q是待测质量的物体(可以被A上的夹子固定).已知该装置的弹簧振子做简谐运动的周期为T=2π| m/k |
①简要写出测量方法及所需测量的物理量(用字母表示)
A.
B.
②用所测物理量和已知物理量求解待测物体质量的计算式为m=
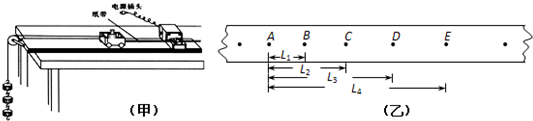
(2)物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关.如图2所示,为了研究某一砂轮的转动动能Ek与角速度ω和关系,可采用下述方法:先让砂轮由动力带动匀速旋转,测行其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下.测出脱离动力到停止转动砂轮转过的转数n,测得几组不同的ω和n如下表所示:
| ω(rad/s) | 0.5 | 1 | 2 | 3 | 4 |
| N | 5 | 20 | 80 | 180 | 320 |
| Ek(J) |
| 10 |
| π |
①试计算出每次脱离动力时砂轮的转动动能,并填入上表中
②试由上述数据推导出该砂轮转动动能Ek与角速度ω的关系式Ek=
③若脱离动力后砂轮角速度为2.5rad/s,则它转过45转后角速度为
分析:(1)根据弹簧振子做简谐运动的周期公式,导出测物体质量的计算式为m=
M,所以要测量的物理量是两个周期;
(2)摩擦力做功,砂轮的动能减小;动能的减小量等于摩擦力做的功;该砂轮转动动能Ek与角速度ω的关系式可以使用图象来处理,也可以使用数据推导.
| ||||
|
(2)摩擦力做功,砂轮的动能减小;动能的减小量等于摩擦力做的功;该砂轮转动动能Ek与角速度ω的关系式可以使用图象来处理,也可以使用数据推导.
解答:解:(1)根据弹簧振子做简谐运动的周期公式:m=
从公式中可以看出,物体的质量与振子的震动周期有关,故需要测量它的振动周期.测量方法及所需测量的物理量:
A、不放Q时用秒表测出振子振动20次(或50次)的时间t1,(或测出振子的周期T1),
B、将Q固定在A上,用秒表测出振子振动20次(或50次)的时间t2,(或测出振子的周期T2)
两次测量对应的公式:M=
①M+m=
②
联立①②式,解得:m=
M
(2)①摩擦力做功,砂轮的动能减小;动能的减小量等于摩擦力做的功,即:EK=F?S=F?N?πD
EK1=F?S=F?N1?πD=0.5J
EK2=F?S=F?N2?πD=2J
EK3=F?S3=F?N3?πD=8J
EK4=F?S4=F?N4?πD=18J
EK5=F?S5=F?N5?πD=32J
②由上述数据可以看出,该砂轮转动动能Ek与角速度ω的平方成正比;任意选取一组数据,得:
=
,所以:EK=2ω2
③砂轮角速度为2.5rad/s时的动能:EK0=2
=12.5J
转过45周,摩擦力做功:W=F?45?πD=4.5J
砂轮剩下的动能:EK=EK0-W=8J
通过上面的表格可以知道,这时的角速度是2rad/s.
故答案为:
(1)①A、不放Q时用秒表测出振子振动20次(或50次)的时间t1,(或测出振子的周期T1),
B、将Q固定在A上,用秒表测出振子振动20次(或50次)的时间t2,(或测出振子的周期T2)
②
M或
M
(2)①0.5,2,8,18,32 ②2ω2 ③2
| kT2 |
| 4π2 |
从公式中可以看出,物体的质量与振子的震动周期有关,故需要测量它的振动周期.测量方法及所需测量的物理量:
A、不放Q时用秒表测出振子振动20次(或50次)的时间t1,(或测出振子的周期T1),
B、将Q固定在A上,用秒表测出振子振动20次(或50次)的时间t2,(或测出振子的周期T2)
两次测量对应的公式:M=
k
| ||
| 4π2 |
k
| ||
| 4π2 |
联立①②式,解得:m=
| ||||
|
(2)①摩擦力做功,砂轮的动能减小;动能的减小量等于摩擦力做的功,即:EK=F?S=F?N?πD
EK1=F?S=F?N1?πD=0.5J
EK2=F?S=F?N2?πD=2J
EK3=F?S3=F?N3?πD=8J
EK4=F?S4=F?N4?πD=18J
EK5=F?S5=F?N5?πD=32J
②由上述数据可以看出,该砂轮转动动能Ek与角速度ω的平方成正比;任意选取一组数据,得:
| EK2 | ||
|
| 2 |
| 1 |
③砂轮角速度为2.5rad/s时的动能:EK0=2
| ω | 2 0 |
转过45周,摩擦力做功:W=F?45?πD=4.5J
砂轮剩下的动能:EK=EK0-W=8J
通过上面的表格可以知道,这时的角速度是2rad/s.
故答案为:
(1)①A、不放Q时用秒表测出振子振动20次(或50次)的时间t1,(或测出振子的周期T1),
B、将Q固定在A上,用秒表测出振子振动20次(或50次)的时间t2,(或测出振子的周期T2)
②
| ||||
|
| ||||
|
(2)①0.5,2,8,18,32 ②2ω2 ③2
点评:这两个实验题目都属于创新性的题目,这类题目首先要理解实验设计的原理,然后根据实验的原理进行解答.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 某同学设计了一种测温装置,其结构如图(a)所示,玻璃泡A内封有一定质量的气体,与A相连的细管B插在水银槽中,管内水银面的高度x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出(B管的体积与A泡的体积相比可略去不计).该同学在某一恒定的大气压下提供不同的环境温度对B管进行温度刻度,测量获得的数据及B管上的温度刻度如下表所示:
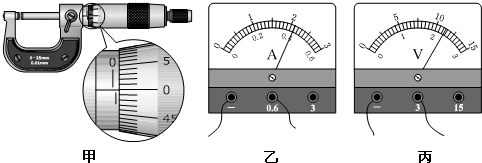
某同学设计了一种测温装置,其结构如图(a)所示,玻璃泡A内封有一定质量的气体,与A相连的细管B插在水银槽中,管内水银面的高度x即可反映泡内气体的温度,即环境温度,并可由B管上的刻度直接读出(B管的体积与A泡的体积相比可略去不计).该同学在某一恒定的大气压下提供不同的环境温度对B管进行温度刻度,测量获得的数据及B管上的温度刻度如下表所示: (量程3V,内阻约3KΩ)
(量程3V,内阻约3KΩ) (量程0.6A,内阻0.01Ω)
(量程0.6A,内阻0.01Ω)