题目内容
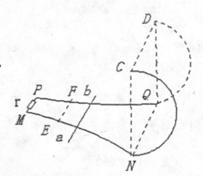
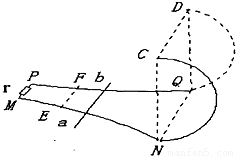
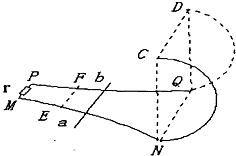 如图,阻值不计的光滑金属导轨MN和PQ水平放置,其最右端NQ间距 d 为 l m,左端MP间接有阻值 r 为 4Ω 的电阻,右端NQ与半径 R 为 2m 的光滑竖直半圆形绝缘导轨平滑连接.在平面NQDC的左侧空间中存在竖直向下的匀强磁场 B,平面NQDC的右侧空间中无磁场.一根阻值不计的长为 L=l.2m,质量 m=0.5kg 的金属杆 ab 放在导轨的 EF 处,EF 与MP平行.现杆 ab 以初速度v0=12m/s 向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置 CD,并恰又落到 EF 位置.求:
如图,阻值不计的光滑金属导轨MN和PQ水平放置,其最右端NQ间距 d 为 l m,左端MP间接有阻值 r 为 4Ω 的电阻,右端NQ与半径 R 为 2m 的光滑竖直半圆形绝缘导轨平滑连接.在平面NQDC的左侧空间中存在竖直向下的匀强磁场 B,平面NQDC的右侧空间中无磁场.一根阻值不计的长为 L=l.2m,质量 m=0.5kg 的金属杆 ab 放在导轨的 EF 处,EF 与MP平行.现杆 ab 以初速度v0=12m/s 向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置 CD,并恰又落到 EF 位置.求:(l)杆ab 刚进入半圆形导轨时,对导轨的压力;
(2)EF 到NQ的距离;
(3)磁感应强度 B 的大小;
(4)试简要说明杆 ab 以初速度v0 向右在水平轨道上做匀减速运动的合理性.
分析:(1)金属杆ab恰能通过最高位置 CD时,由重力提供向心力,根据牛顿第二定律可求出经过最高点的速度.棒从NQ到最高点的过程机械能守恒,则可求出棒通过NQ时的速度.棒经NQ时,由重力和轨道的支持力提供其向心力,由牛顿运动定律求出杆ab刚进入半圆形导轨时对导轨的压力.
(2)ab 离开半圆形导轨后做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,由下落的高度为2R和最高点的速度结合可求出EF到NQ的距离;
(3)杆 ab 做匀减速运动,由运动学公式、牛顿第二定律和安培力结合可求得B.
(4)杆向右运动时,受到向左的安培力作用,使杆的运动速度v减小,而随着轨道宽度变大,L变大,由FA=
可知,杆所受的安培力有可能不变,则棒可以做匀减速运动.
(2)ab 离开半圆形导轨后做平抛运动,水平方向做匀速直线运动,竖直方向做自由落体运动,由下落的高度为2R和最高点的速度结合可求出EF到NQ的距离;
(3)杆 ab 做匀减速运动,由运动学公式、牛顿第二定律和安培力结合可求得B.
(4)杆向右运动时,受到向左的安培力作用,使杆的运动速度v减小,而随着轨道宽度变大,L变大,由FA=
| B2L2v |
| R |
解答:解:( 1 )设杆ab刚进入半圆形导轨时速度为v1,到达最高位置时速度为v2,由于恰能通过最高点,则:
mg=
得:v2=2
m/s
杆ab进入半圆形导轨后,由于轨道绝缘,无感应电流,则根据机械能守恒定律:
m
=mg?2R+
m
解得:v1=10m/s
设在最低点时半圆形轨道对杆ab的支持力为 N
N-mg=
得:N=30N
( 2 )ab离开半圆形导轨后做平抛运动,设经时间t落到水平导轨上
由
gt2=2R得,t=
S
则EF与NQ的水平距离 S=v2t=4 m
(3)设杆ab做匀减速运动的加速度为a
-
=2as得:a=-5.5m/s2
对杆刚要到达NQ位置处进行分析:
由FA=BId、I=
得
B=
=
T≈1.05T
(4)杆向右运动时,受到向左的安培力作用,使杆的运动速度v减小,而随着轨道宽度变大,L变大,由FA=
可知,杆所受的安培力有可以不变,故杆作匀减速运动是合理的.
答:
(l)杆ab刚进入半圆形导轨时,对导轨的压力为30N;
(2)EF 到NQ的距离为4m;
(3)磁感应强度B的大小为1.05T;
(4)杆向右运动时,受到向左的安培力作用,使杆的运动速度v减小,而随着轨道宽度变大,L变大,由FA=
可知,杆所受的安培力有可以不变,故杆作匀减速运动是合理的.
mg=
| mv22 |
| R |
| 5 |
杆ab进入半圆形导轨后,由于轨道绝缘,无感应电流,则根据机械能守恒定律:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
解得:v1=10m/s
设在最低点时半圆形轨道对杆ab的支持力为 N
N-mg=
m
| ||
| R |
( 2 )ab离开半圆形导轨后做平抛运动,设经时间t落到水平导轨上
由
| 1 |
| 2 |
2
| ||
| 5 |
则EF与NQ的水平距离 S=v2t=4 m
(3)设杆ab做匀减速运动的加速度为a
| v | 2 1 |
| v | 2 0 |
对杆刚要到达NQ位置处进行分析:
由FA=BId、I=
| Bdv1 |
| r |
B=
|
| 1.1 |
(4)杆向右运动时,受到向左的安培力作用,使杆的运动速度v减小,而随着轨道宽度变大,L变大,由FA=
| B2L2v |
| R |
答:
(l)杆ab刚进入半圆形导轨时,对导轨的压力为30N;
(2)EF 到NQ的距离为4m;
(3)磁感应强度B的大小为1.05T;
(4)杆向右运动时,受到向左的安培力作用,使杆的运动速度v减小,而随着轨道宽度变大,L变大,由FA=
| B2L2v |
| R |
点评:本题的突破口是棒恰能通过最高位置CD,达到临界状态,由牛顿第二定律可求得临界速度.本题是电磁感应中的力学问题,安培力的分析和计算是关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2009?宁波模拟)如图,阻值不计的光滑金属导轨MN和PQ 水平放置,其最右端间距d为1m,左端MP接有阻值r为4Ω的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为 L=l.2m,质量 m=0.5kg 的金属杆 ab 放在导轨的 EF 处,EF 与MP平行.在平面NQDC的左侧空间中存在竖直向下的匀强磁场 B,平面NQDC的右侧空间中无磁场.现杆 ab 以初速度V0=12m/s 向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置 CD 并恰又落到 EF 位置;(g取10m/s2 ) 求:
(2009?宁波模拟)如图,阻值不计的光滑金属导轨MN和PQ 水平放置,其最右端间距d为1m,左端MP接有阻值r为4Ω的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为 L=l.2m,质量 m=0.5kg 的金属杆 ab 放在导轨的 EF 处,EF 与MP平行.在平面NQDC的左侧空间中存在竖直向下的匀强磁场 B,平面NQDC的右侧空间中无磁场.现杆 ab 以初速度V0=12m/s 向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置 CD 并恰又落到 EF 位置;(g取10m/s2 ) 求: 的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为L=1.2m,质量m=0.5kg的金属杆ab放在导轨的EF处,EF与NQ平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场B,平面NQDC的右侧空间中无磁场。现杆ab以初速度v0=12m/s向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置CD并恰又落到EF位置; (g取10m/s2)
的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为L=1.2m,质量m=0.5kg的金属杆ab放在导轨的EF处,EF与NQ平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场B,平面NQDC的右侧空间中无磁场。现杆ab以初速度v0=12m/s向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置CD并恰又落到EF位置; (g取10m/s2)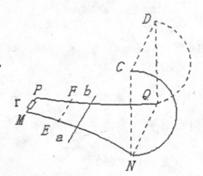
 的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为L=1.2m,质量m=0.5kg的金属杆ab放在导轨的EF处,EF与NQ平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场B,平面NQDC的右侧空间中无磁场。现杆ab以初速度v0=12m/s向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置CD并恰又落到EF位置; (g取10m/s2)
的电阻,右端NQ与半径R为2m的光滑竖直半圆形绝缘导轨平滑连接;一根阻值不计的长为L=1.2m,质量m=0.5kg的金属杆ab放在导轨的EF处,EF与NQ平行。在平面NQDC的左侧空间中存在竖直向下的匀强磁场B,平面NQDC的右侧空间中无磁场。现杆ab以初速度v0=12m/s向右在水平轨道上做匀减速运动,进入半圆形导轨后恰能通过最高位置CD并恰又落到EF位置; (g取10m/s2)