题目内容
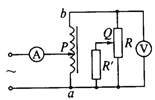
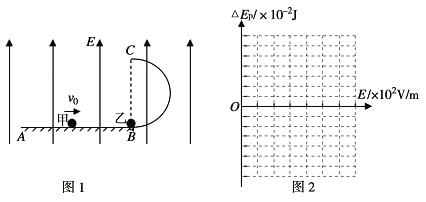
【题目】如图甲所示，真空中存在电场强度 
、方向竖直向上的匀强电场.在电场中固定有竖直面内的光滑绝缘轨道ABC，其中AB段水平，BC段是半径
的半圆，直径BC竖直.甲、乙是两个完全相同的导体小球(均可视为质点)，质量均为
。甲球电量为
、乙球不带电.开始时，乙球静止于B点.甲球在水平轨道上以初速度
向右运动，与乙球发生时间极短的弹性正碰。碰撞后乙球沿圆轨道运动到C点后水平抛出，落到水平轨道AB上的D点位置。取
，求：
（1）甲、乙两球碰撞后瞬间，乙球的速度
的大小；
（2）小球乙落在D点时，甲、乙两小球之间的距离S；
（3）若只改变场强E的大小，为了保证乙球能沿竖直轨道运动，并通过C点后落到水平轨道AB上，试确定场强E的取值范围.设乙球从B点运动到C的过程中，电势能的变化量为
，在图2的坐标系中，定量画出小球乙的电势能变化量
与场强E的关系图象.(画图时不必说明理由)
【答案】（1）
（2）2m（3）
；
【解析】试题分析：小球1、2发生弹性正碰，动量守恒，机械能守恒，结合动量守恒定律和机械能守恒定律求出碰撞后瞬间小球2的速度．根据动能定理求出小球2通过C点的速度，结合牛顿第二定律求出轨道对它的压力大小，小球2离开C点后做类平抛运动，结合牛顿第二定律求出加速度，求出竖直方向上的运动时间，通过等时性求出水平方向上的位移．为了保证小球2能沿轨道运动并通过C点，通过C点时压力大于等于零，以及抓住电场力小于重力，结合动能定理求出电场强度的范围．由电场力做功与电势能变化之间的关系可求出
的最大值和最小值，作出
E图象
（1）设甲小球和乙小球碰撞后的速度分别为
和
，
由于动量守恒和机械能守恒： 
…①，
…②
解得
③
甲球和乙球碰撞后电量均为
…④
（2）设乙球经过C点速度为
，由动能定理得： 
…⑤
解得
⑥
由向心力公式得
…⑦，解得
…⑧
乙球离开C点后做类似平抛运动，加速度为a，运动时间为t，水平位移为x：
根据牛顿第二定律可得
⑨，
…⑩，
…
解得x=2m…
（3）乙球能够运动到C点的条件是
…
联立（5）、（7）、（13）解得：场强的最小值为
…
乙球离开C点后落到轨道AB上，需满足的条件是
…
解得场强的最大值为
…
所以场强的取值范围为
…
乙球由B点沿轨道运动至C点的过程中，电场力做正功，电势能减小
…
解得： 
， 
…
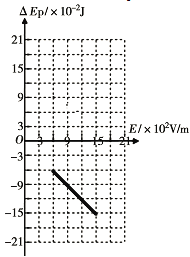
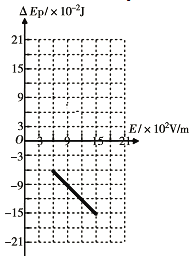
其电势能变化量
与场强E的关系图象如图所示．
口算题卡北京妇女儿童出版社系列答案
