题目内容

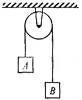
如图所示，两个质量各为mA和mB的小球A和B，分别系在一条跨过定滑轮的柔软轻绳的两端，不计滑轮轴的摩擦、滑轮的质量和空气阻力，已知mA＞mB，开始时，A、B两球以等大的初速度V0分别竖直向下和竖直向上运动，当A物体下降距离为h时，A、B速度大小都为Vt，试利用牛顿运动定律及匀变速直线运动规律，证明在此运动过程中，A、B组成的系统机械能守恒。
解：设A、B两球组成整体加速度大小a, 对A、B两球组成的系统，在沿着绳子方向上，由牛顿第二定律得： 
（mA-mB）g=（mA+mB）a ①
对于A球，由匀变速直线运动位移公式有： 
h=(Vt2-V02)/2a ②
在此过程中，A、B组成的系统的总的重力势能减少量为△Ep=（mA-mB）gh ③
A、B组成的系统的总动能增加量为△Ek=（mA+mB）(Vt2-V02)/2 ④
由①～④解得：△Ep+△Ep=0 
即A、B组成的系统的总机械能守恒 
练习册系列答案
相关题目
如图所示，两个质量各为m1和m2的小物块A和B，分别系在一条跨过定滑轮的软绳两端，已知m1＞m2．现要利用此装置验证机械能守恒定律．
（1）若选定物块A从静止开始下落的过程进行测量，则需测量的物理量有
．
①物块的质量m1、m2；
②物块A下落的距离及下落这段距离所用的时间；
③物块B上升的距离及上升这段距离所用的时间；
④绳子的长度．
（2）为提高实验结果的准确程度．某小组同学对此实验提出如下建议：
①绳的质量要轻；
②在“轻质绳”的前提下绳子越长越好；
③尽量保证物块沿竖直方向运动，不要摇晃；
④两个物块的质量之差要尽可能小．
以上建议中对提高准确程度确实有作用的是
．
（3）写出一条上面没有提到的对提高实验结果准确程度有益的建议：
．
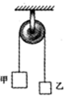如图所示，两个质量各为m1和m2的小物块甲和乙，分别系在一条跨过定滑轮的轻绳两端，已知，m1：m2=3：1，不计摩擦，g=10m/s2，则甲乙运动时加速度的大小为
5
5
m/s2．
（2010?宿州二模）如图所示，两个质量各为mA和mB的小球A和B，分别系在一条跨过定滑轮的柔软轻绳的两端，不计滑轮轴的摩擦、滑轮的质量和空气阻力，已知mA＞mB，开始时，A、B两球以等大的初速度V0分别竖直向下和竖直向上运动，当A物体下降距离为h时，A、B速度大小都为Vt，试利用牛顿运动定律及匀变速直线运动规律，证明在此运动过程中，A、B组成的系统机械能守恒．

如图所示，两个质量各为m1、m2的小物块A和B, 分别系在一条跨过定滑轮的软绳两端, 已知m1>m2. 现要利用此装置验证机械能守恒定律。

（1）若选定物块A从静止开始下落的过程进行测量, 则需要测量的物理量有_________.(在横线上填入选项前的编号)
①物块的质量m1、m2；
②物块A下落的距离及下落这段距离所用的时间；
③物块B上升的距离及上升这段距离所用的时间；
④绳子的长度。
（2）为提高实验结果的准确程度, 某小组同学对此实验提出以下建议：
①绳的质量要轻；
②在“轻质绳”的前提下，绳子越长越好；
③尽量保证物块只沿竖直方向运动，不要摇晃
④两个物块的质量之差要尽可能小。
以上建议中确实对提高准确度有作用的是____________。（在横线上填入选项前的编号）
（3）写出一条上面没有提到的对提高实验结果准确程度有益的建议：_________________________________________________________________________。

如图所示，两个质量各为m1和m2的小物块A和B，分别系在一条跨过定滑轮的轻软绳两端，已知m1＞m2，现要利用此装置验证机械能守恒定律。

（1）若选定物块A从静止开始下落的过程进行测量，则需要测量的物理量有         （在答题卡上对应区域填入选项前的编号）
①物块的质量m1、m2；
②物块A下落的距离及下落这段距离所用的时间；
③物块B上升的距离及上升这段距离所用的时间；
④绳子的长度。
（2）为提高实验结果的准确程度，某小组同学对此实验提出以下建议：
①绳的质量要轻：
②在“轻质绳”的前提下，绳子越长越好；
③尽量保证物块只沿竖直方向运动，不要摇晃；
④两个物块的质量之差要尽可能小。
以上建议中确实对提高准确程度有作用的是              。（在答题卡上对应区域填入选项前的编号）
（3）写出一条上面没有提到的提高实验结果准确程度有益的建议：                                                    
                                                               。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网