题目内容
 (2010?宿州二模)如图所示,两个质量各为mA和mB的小球A和B,分别系在一条跨过定滑轮的柔软轻绳的两端,不计滑轮轴的摩擦、滑轮的质量和空气阻力,已知mA>mB,开始时,A、B两球以等大的初速度V0分别竖直向下和竖直向上运动,当A物体下降距离为h时,A、B速度大小都为Vt,试利用牛顿运动定律及匀变速直线运动规律,证明在此运动过程中,A、B组成的系统机械能守恒.
(2010?宿州二模)如图所示,两个质量各为mA和mB的小球A和B,分别系在一条跨过定滑轮的柔软轻绳的两端,不计滑轮轴的摩擦、滑轮的质量和空气阻力,已知mA>mB,开始时,A、B两球以等大的初速度V0分别竖直向下和竖直向上运动,当A物体下降距离为h时,A、B速度大小都为Vt,试利用牛顿运动定律及匀变速直线运动规律,证明在此运动过程中,A、B组成的系统机械能守恒.分析:A、B两球以等大的初速度V0分别竖直向下和竖直向上运动,根据牛顿第二定律求出两者的加速度大小,由运动学公式得到h与速度vt和v0的关系,可求出A、B组成的系统的总的重力势能减少量△Ep,以及总动能的增加量△Ek,若△Ep+△Ep=0,证明系统的总机械能守恒.
解答:解:设A、B两球组成整体加速度大小a.
对A、B两球组成的系统,在沿着绳子方向上,由牛顿第二定律得:
(mA-mB)g=(mA+mB)a
对于A球,由匀变速直线运动位移公式有:h=
在此过程中,A、B组成的系统的总的重力势能减少量为:△Ep=(mA-mB)gh
联立以上三式得:△Ep=-
(mA+mB)(vt2-v02)
A、B组成的系统的总动能增加量为:△Ek=
(mA+mB)(vt2-v02)
解得:△Ep+△Ep=0
即A、B组成的系统的总机械能守恒
答:证明在此运动过程中,A、B组成的系统机械能守恒见上.
对A、B两球组成的系统,在沿着绳子方向上,由牛顿第二定律得:
(mA-mB)g=(mA+mB)a
对于A球,由匀变速直线运动位移公式有:h=
| ||||
| 2a |
在此过程中,A、B组成的系统的总的重力势能减少量为:△Ep=(mA-mB)gh
联立以上三式得:△Ep=-
| 1 |
| 2 |
A、B组成的系统的总动能增加量为:△Ek=
| 1 |
| 2 |
解得:△Ep+△Ep=0
即A、B组成的系统的总机械能守恒
答:证明在此运动过程中,A、B组成的系统机械能守恒见上.
点评:运用常见的运动证明机械能守恒是常见的题型,本题关键求得加速度,得到h与速度的关系式.

练习册系列答案
相关题目
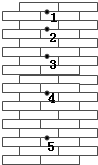 (2010?宿州二模)如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5、…所示下落小球运动过程中每次曝光的位置.已知连续两次曝光的时间间隔均为T,每块砖的厚度均为d,该同学没有查到当地重力加速度值,根据图上的信息和已知条件,下列判断正确的是( )
(2010?宿州二模)如图所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5、…所示下落小球运动过程中每次曝光的位置.已知连续两次曝光的时间间隔均为T,每块砖的厚度均为d,该同学没有查到当地重力加速度值,根据图上的信息和已知条件,下列判断正确的是( )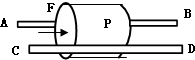 (2010?宿州二模)如图所示,两根相同的粗糙均匀的木棍AB和CD相互平行,固定在同一个水平面上.一个外面粗糙均匀的圆柱形工件P架在两木棍之间,在沿中心轴线水平向右的推力F的作用下,恰好能向右匀速运动(设最大静摩擦力等于滑动摩擦力).若保持两木棍在同一水平面内,但将它们的距离稍微减小一些后固定.仍将圆柱工件P架在两木棍之间静止不动,再用同样的水平力F向右推该工件,则下列说法中正确的是( )
(2010?宿州二模)如图所示,两根相同的粗糙均匀的木棍AB和CD相互平行,固定在同一个水平面上.一个外面粗糙均匀的圆柱形工件P架在两木棍之间,在沿中心轴线水平向右的推力F的作用下,恰好能向右匀速运动(设最大静摩擦力等于滑动摩擦力).若保持两木棍在同一水平面内,但将它们的距离稍微减小一些后固定.仍将圆柱工件P架在两木棍之间静止不动,再用同样的水平力F向右推该工件,则下列说法中正确的是( )