题目内容
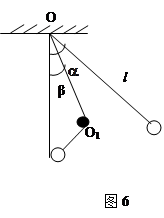
（7分）如图6所示，质量为m的小球，用不可伸长的线悬于固定点O，线长为l，初始线与铅垂线有一个夹角，初速为0. 在小球开始运动后，线碰到铁钉O1. 铁钉的方向与小球运动的平面垂直. OO1=h<l，且已知OO1与铅垂线夹角为β. 假设碰后小球恰能做圆周运动. 求线与铁钉碰前瞬时与碰后瞬时张力的变化.
假设碰后小球能作圆周运动，运动到最高点的速度
可由
（1分）
得出
设初始夹角为α
由机械能守恒得到：
（2分）
假设碰前瞬时速度为v1
则：
（1分）
碰前：
（1分）
（1分）
（1分）
本题考查圆周运动和机械能守恒的综合应用，在最高点恰好通过，说明只有重力提供向心力，可求得最高点速度大小，小球碰后到最高点，绳子的拉力不做功，所以小球机械能守恒，规定最低点为零势面，列方程求解，根据碰前碰后拉力和重力分力提供向心力列式求解
可由（1分）
得出
设初始夹角为α
由机械能守恒得到：
（2分） 假设碰前瞬时速度为v1
则：
（1分）碰前：
（1分） （1分） （1分）本题考查圆周运动和机械能守恒的综合应用，在最高点恰好通过，说明只有重力提供向心力，可求得最高点速度大小，小球碰后到最高点，绳子的拉力不做功，所以小球机械能守恒，规定最低点为零势面，列方程求解，根据碰前碰后拉力和重力分力提供向心力列式求解
练习册系列答案
阅读快车系列答案
相关题目
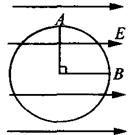
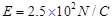、方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线一端固定于O点，另一端拴着质量m=0.5kg、电荷量
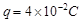的小球。现将细线拉至水平位置，将小球由静止释放，当小球运动到最高点时细线受到的拉力恰好达到它能承受的最大值而断裂，取
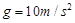。求：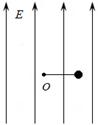
＝90°时，重力对b球做功的瞬时功率为多少？a球对地面的压力为多少？
= 。
CD