题目内容
轻杆可绕其一端为轴自由转动，在杆的中点和另一端分别固定质量为2m、m的两个小球，如图所示，将该装置从水平位置由静止释放，刚好转动到竖直位置时，质量为m的小球突然脱落，则（ ）| A、其余部分不能达到水平位置 | B、其余部分仍能刚好达到水平位置 | C、其余部分能达到水平位置以上，但不能达到竖直位置 | D、其余部分可以绕轴在竖直面内做圆周运动 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
平抛物体的运动规律可以概括为两点：①水平方向做匀速直线运动；②竖直方向做自由落体运动．为了研究平抛物体的运动，可做下面的实验：如图所示，用小锤打击弹性金属片，A球就水平飞出，同时B球被松开，做自由落体运动，两球同时落到地面．这个实验（ ）| A、不能说明上述规律中的任何一条 | B、能同时说明上述两条规律 | C、只能说明上述规律中的第①条 | D、只能说明上述规律中的第②条 |
如图，是一个匀速转动的电扇，O为转动轴，A、B为电扇上两个质点，下列说法正确的是（ ）| A、电扇在做匀速圆周运动 | B、电扇在绕O轴匀速转动 | C、电扇上A、B两个质点都在做匀速圆周运动 | D、电扇上A、B两个质点角速度相同 |
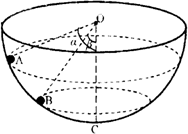如图所示，有一固定的且内壁光滑的半球面，球心为O．最低点为C，在其内壁上有两个质量相同的小球（可视为质点）A和B，在两个高度不同的水平面内做匀速圆周运动，A球的轨迹平面高于B球的轨迹平面．A、B两球与O点的连线与竖直线OC间的夹角分别为α=53°和β=37°，以最代点C所在的水平面为重力势能的参考平面，则（ ）（sin37°=| 3 |
| 5 |
| 4 |
| 5 |
| A、A、B两球所受弹力的大小之比为4：3 |
| B、A、B两球运动的周期之比为4：3 |
| C、A、B两球的动能之比为64：27 |
| D、A、B两球的重力势能之比为16：9 |
利用双线可以稳固小球在竖直平面内做圆周运动而不易偏离竖直面，如图，用两根长为L的细线系一质量为m的小球，两线上端系于水平横杆上，A、B两点相距也为L，若小球恰能在竖直面内做完整的圆周运动，则小球运动到最低点时，每根线承受的张力为（ ）A、2
| ||||
| B、3mg | ||||
| C、2.5mg | ||||
D、
|
关于公式
=k，下列说法正确的是（ ）
| a3 |
| t2 |
| A、围绕同一星球运行的星星或卫星，k值不相等 |
| B、围绕不同星球运行的星星或卫星，k值均相等 |
| C、公式只适用于围绕太阳运行的行星 |
| D、以上说法均错误 |
科学家在望远镜中看到太阳系外某一恒星有一行星，并测得它围绕该恒星运行一周所用的时间为1200年，它与该恒星的距离为地球到太阳距离的100倍． 假定该行星绕恒星运行的轨道和地球绕太阳运行的轨道都是圆周，仅利用以上两个数据可以求出的量有（ ）
| A、行星质量与太阳质量之比 | B、恒星密度与太阳密度之比 | C、行星质量与地球质量之比 | D、行星运行速度与地球公转速度之比 |
为了探测x星球，载着登陆舱的探测飞船在该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1，总质量为m1．随后登陆舱脱离飞船，变轨到离星球更近的半径为r2的圆轨道上运动，此时登陆舱的质量为m2，则（ ）
A、x星球的质量为M=
| ||||||||
B、x星球表面的重力加速度为gx=
| ||||||||
C、登陆舱在r1与r2轨道上运动时的速度大小之比为
| ||||||||
D、登陆舱在半径为r2轨道上做圆周运动的周期为T2=T1
|
2012年6月15日，“蛟龙号”载人潜水器在西太平洋进行第一次下潜试验，最大下潜深度约为6.4km．假设地球是一半径R=6400km、质量分布均匀的球体．已知质量分布均匀的球壳对壳内物体的引力为零．则“蛟龙号”在最大下潜深度处的重力与海面上的重力之比约为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|