题目内容
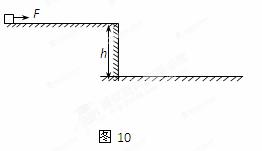
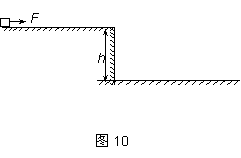
如图10所示，质量m＝1 kg的小物块放在一质量为M＝4 kg的足够长的木板右端，物块与木板间的动摩擦因数μ＝0.2，木板与水平面间的摩擦不计。物块用劲度系数k＝25 N/m的弹簧拴住，弹簧的左端固定(与木板不粘连)。开始时整个装置静止，弹簧处于原长状态。现对木板施以12 N的水平向右的恒力(物块与木板间最大静摩擦力可认为等于滑动摩擦力，g＝10 m/s2)。已知弹簧的弹性势能Ep＝
kx2，式中x为弹簧的伸长量或压缩量。求：
(1)开始施力的瞬间小物块的加速度；
(2)物块达到的最大速度是多少？
图10
解析：(1)假设m、M相对静止，由牛顿第二定律
a＝
＝2.4 m/s2。
此时m受的合外力
F合＝ma＝2.4 N>Ff＝μmg＝2 N。
所以m、M相对滑动a＝
＝μg＝2 m/s2。
(2)速度最大时，物块所受合力为零，此时弹簧伸长x，则kx＝μmg，
所以x＝0.08 m，由功能关系
μmgx＝kx2＋mvm2。
所以vm＝0.4 m/s。
答案：(1)2 m/s2 (2)0.4 m/s
练习册系列答案
相关题目
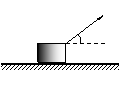如图 10 所示，质量m = 2kg 的物体静止在水平地面上，物体与地面间的动摩擦因数μ = 0.75。一个与水平方向成 37°角斜向上、大小F = 20N 的力拉物体，
