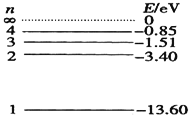
题目内容
【题目】如图甲是一种利用磁场偏转的粒子收集装置原理图。两块磁铁前后平行垂直水平面放置,收集板位于两块磁铁之间,平行于上下底面从高到低依次放置,所有收集板的右端在同一竖直面上,收集板长度从高到低依次变大,因而左端位置不同。已知两磁铁之间的长方体空间内存在水平方向的匀强磁场,磁感应强度为B=0.1T。一个粒子源被固定在其底面上,粒子源竖直向上发射出质量为![]() kg、电荷量绝对值为
kg、电荷量绝对值为![]() C、动能不同的粒子,这些粒子进入磁场后,在磁场的作用下运动,并打到右侧的多片收集板上(如图乙中D1、D2、D3所示)。收集板D1刚好与粒子出射点在同一高度,已知收集板D1、D2、D3收集的最小粒子动能分别为
C、动能不同的粒子,这些粒子进入磁场后,在磁场的作用下运动,并打到右侧的多片收集板上(如图乙中D1、D2、D3所示)。收集板D1刚好与粒子出射点在同一高度,已知收集板D1、D2、D3收集的最小粒子动能分别为![]() eV、
eV、![]() eV、
eV、![]() eV。粒子击中收集板后有一定比例反射,反射前后粒子速度方向与收集板平面的夹角大小不变,反射速度最大值为撞击前速度的k=0.6倍。重力及粒子间的相互作用忽略不计。
eV。粒子击中收集板后有一定比例反射,反射前后粒子速度方向与收集板平面的夹角大小不变,反射速度最大值为撞击前速度的k=0.6倍。重力及粒子间的相互作用忽略不计。
(1)试判断粒子的电性,并写出粒子在磁场中运动的半径r与动能Ek的关系式(用q,m,B表示);
(2)计算D1板左端到粒子源的水平距离s1,并讨论要使得能量在ED1与ED2之间的粒子最终全部被D1吸收,D1板至少多长(左端到右端的距离);
(3)为了使粒子在撞击收集板反弹后不会碰到其他收集板,D2、D3到D1竖直距离的最小值分别为多少?并算出此时D2的左端到粒子源的水平距离s2。

【答案】(1)负电;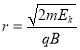 ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)粒子在垂直纸面向内的磁场中向右偏,由左手定则判断,粒子带负电,洛伦兹力提供向心力
![]()
动能![]() ,得
,得
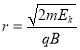
(2)由上小题知
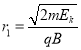
![]()
代入数据得
![]() m
m
打到D1的最大动能的临界是![]() eV,其对应的半径
eV,其对应的半径![]() m
m
因此其第一次在D1上的落点到粒子源的距离为
![]()
这些粒子中反弹的粒子速度最大为原来的k倍,故半径为原来的k倍
因此这些反射的粒子不断的向右以半圆的轨迹运动,半径按k倍减小,经无穷多次碰撞后,粒子到粒子源的距离
![]()
因此D1的板长至少为
![]()
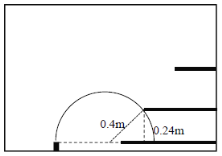
(3)粒子在D1板中碰撞后反弹,到达的最大高度为
![]()
此即D2板距D1板的最短距离。如图所示,由三角形知,底边长为0.32m,D2左端点到粒子源的距离
![]()
打在D2板上速度最大的粒子,恰好经过D3板左边缘,其半径为![]()
打在D2板上反射后,其半径变为![]()
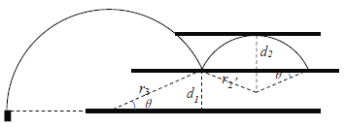
其轨迹最高点到向上最大距离d2可由两相似三角形关系表示,即
![]()
解得![]() ;
;
故D3板到D1板的距离至少为
![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案