题目内容
【题目】在边长为
L的等边三角形ABC范围内存在着垂直纸面向里的匀强磁场，磁感应强度为B。位于等边三角形中心O处的粒子源可向纸面内的各个方向发射速率相等的同种带正电粒子，粒子的比荷为
，不计重力及粒子间的相互作用。
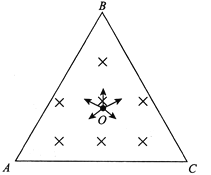
(1)若等边三角形AB边的任意位置都会有粒子通过，求粒子初速度的大小应满足的条件。
(2)若粒子的初速度大小为v0时，恰好可使等边三角形AB边的任意位置都会有粒子通过，求初速度为v0的粒子在磁场中运动时间最长与最短的差值。(已知：若sinθ=k，则θ=arcsin k)
【答案】(1) 
(2) 
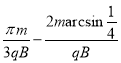
【解析】由几何关系可知AO=BO=CO=
Lsin600
=L，为保证等边三角形AB边的任意位置都会有粒子通过，粒子圆周运动轨迹必须进过A点和B点，如图；
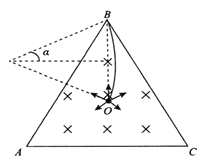
满足条件的粒子半径为
其中
，解得R≥L
洛伦兹力提供向心力qvB=m
解得
（2）粒子的初速度大小为v0时，恰好可使等边三角形AB边的任意位置都会有粒子通过，则
此时粒子圆周运动的半径为R=L轨迹恰通过各边中点的粒子，在磁场中运动时间最短，如图；
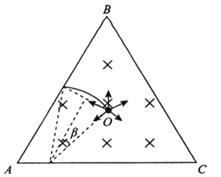
由几何关系：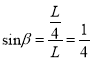 
粒子在磁场中运动的时间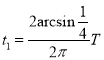
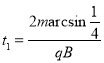
轨迹恰好通过A点、B点或C点的粒子，在磁场中运动的时间最长，如图；
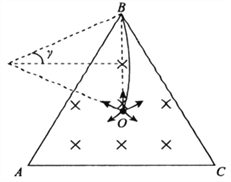
由几何关系可知，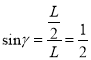 
粒子在磁场中运动最长与最短时间差值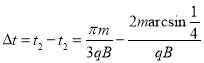
练习册系列答案
相关题目
