题目内容
如图所示，小球在水平推力F的作用下静止在固定的光滑斜面上，已知小球重力为G，斜面倾角为θ，则斜面对小球的弹力大小为（ ）分析：分析小球的受力情况，作出力图，分别运用合成法和正交分解法得出斜面对小球的弹力大小．
解答：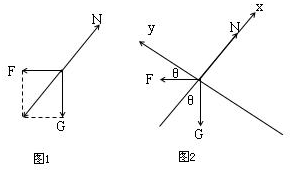
解：分析小球的受力情况：重力G、水平推力F和斜面的支持力N，作出力图．
根据平衡条件得知，F、G的合力与N大小相等、方向相反，作出F、G的合力如图1所示，则有
N=
又根据正交分解法，如图2建立坐标系，由平衡条件得：
N=Gcosθ+Fsinθ
故选AB
解：分析小球的受力情况：重力G、水平推力F和斜面的支持力N，作出力图．根据平衡条件得知，F、G的合力与N大小相等、方向相反，作出F、G的合力如图1所示，则有
N=
| G2+F2 |
又根据正交分解法，如图2建立坐标系，由平衡条件得：
N=Gcosθ+Fsinθ
故选AB
点评：对于三个力的平衡问题，常常有三个方法处理：1、合成法；2、正交分解法；3、分解法．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
如图所示，小球在水平推力F的作用下静止在光滑的斜面上，已知小球重为G，斜面倾角为θ，则斜面对小球的弹力大小为（ ）
如图所示，小球在水平恒力F作用下，由静止开始从A点出发沿光滑水平面AB做直线运动，到B点时速度达到VB=
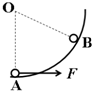如图所示，小球在水平拉力作用下，以恒定速率v沿竖直光滑圆轨由A点运动到B点，在此过程中拉力的瞬时功率变化情况是（ ）| A、逐渐减小 | B、逐渐增大 | C、先减小，后增大 | D、先增大，后减小 |
