题目内容
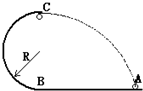 如图所示,小球在水平恒力F作用下,由静止开始从A点出发沿光滑水平面AB做直线运动,到B点时速度达到VB=
如图所示,小球在水平恒力F作用下,由静止开始从A点出发沿光滑水平面AB做直线运动,到B点时速度达到VB=| 5gR |
(1)小球运动到C点时的速度;
(2)小球在AB间运动过程中受到的恒力F.
分析:(1)小球在C处,恰能做圆周运动,则有mg=
,可求得小球在C点的速度VC.
(2)小球从C到A做平抛运动,根据平抛运动的规律列式,联立方程即可求出AB间的距离.再对于小球由A到B做匀加速运动过程,运用牛顿第二定律和运动学公式结合或动能定理列式,求解F的大小.
m
| ||
| R |
(2)小球从C到A做平抛运动,根据平抛运动的规律列式,联立方程即可求出AB间的距离.再对于小球由A到B做匀加速运动过程,运用牛顿第二定律和运动学公式结合或动能定理列式,求解F的大小.
解答:解:(1)设小球在C点的速度为VC.在C点,由重力提供向心力,则有:mg=
得:Vc=
(2)小球由C点开始做平抛运动,设经过时间t到达A点,则有:
竖直方向:2R=
gt2…①
水平方向:xAB=VCt…②
小球由A到B做匀加速运动:
由
=2axAB…③
根据牛顿第二定律得:F=ma …④
由①②③④得:F=
mg
答:(1)小球运动到C点时的速度为
;
(2)小球在AB间运动过程中受到的恒力F为
mg.
m
| ||
| R |
得:Vc=
| gR |
(2)小球由C点开始做平抛运动,设经过时间t到达A点,则有:
竖直方向:2R=
| 1 |
| 2 |
水平方向:xAB=VCt…②
小球由A到B做匀加速运动:
由
| V | 2 B |
根据牛顿第二定律得:F=ma …④
由①②③④得:F=
| 5 |
| 4 |
答:(1)小球运动到C点时的速度为
| gR |
(2)小球在AB间运动过程中受到的恒力F为
| 5 |
| 4 |
点评:本题主要考查了向心力公式、平抛运动基本公式、牛顿第二定律及运动学基本公式的直接应用,涉及的知识点较多,关键要掌握每个过程的物理规律.

练习册系列答案
相关题目
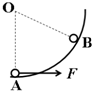 如图所示,小球在水平拉力作用下,以恒定速率v沿竖直光滑圆轨由A点运动到B点,在此过程中拉力的瞬时功率变化情况是( )
如图所示,小球在水平拉力作用下,以恒定速率v沿竖直光滑圆轨由A点运动到B点,在此过程中拉力的瞬时功率变化情况是( )| A、逐渐减小 | B、逐渐增大 | C、先减小,后增大 | D、先增大,后减小 |
 如图所示,小球在水平推力F的作用下静止在固定的光滑斜面上,已知小球重力为G,斜面倾角为θ,则斜面对小球的弹力大小为( )
如图所示,小球在水平推力F的作用下静止在固定的光滑斜面上,已知小球重力为G,斜面倾角为θ,则斜面对小球的弹力大小为( ) 如图所示,小球在水平推力F的作用下静止在光滑的斜面上,已知小球重为G,斜面倾角为θ,则斜面对小球的弹力大小为( )
如图所示,小球在水平推力F的作用下静止在光滑的斜面上,已知小球重为G,斜面倾角为θ,则斜面对小球的弹力大小为( )