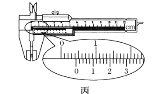
题目内容
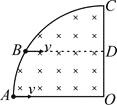
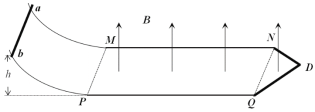
【题目】如图所示,两彼此平行的金属导轨MN、PQ水平放置,左端与一光滑绝缘的曲面相切,右端接一水平放置的光滑“>”形金属框架NDQ,∠NDQ=1200,ND与DQ的长度均为L,MP右侧空间存在磁感应强度大小为B、方向竖直向上的匀强磁场。导轨MN、PQ电阻不计,金属棒与金属框架NDQ单位长度的电阻值为r,金属棒质量为m,长度与MN、PQ之间的间距相同,与导轨MN、PQ的动摩擦因数为。现让金属棒从曲面上离水平面高h的位置由静止释放,金属棒恰好能运动到NQ边界处。
(1)刚进入磁场时回路的电流强度i0;
(2)棒从MP运动到NQ所用的时间为t,求导轨MN、PQ的长度s;
(3)棒到达NQ后,施加一外力使棒以恒定的加速度a继续向右运动,求此后回路中电功率的最大值pmax。
【答案】![]() ;
;![]() ;
;![]()
【解析】
解:(1)金属棒从光滑绝缘曲面向下运动,机械能守恒,设刚进入MP边界时,速度大小为![]() ,则:
,则:![]()
解得:![]()
刚进入磁场时产生的感应电动势:![]()
导轨宽度:![]()
回路电阻:![]()
联立可得:![]()
(2)设长度为S,从MP到NQ过程中的任一时刻,速度为![]() ,在此后无穷小的
,在此后无穷小的![]() 时间内,根据动量定理:
时间内,根据动量定理:![]()
![]()
![]()
![]()
得:![]()
(3)金属棒匀加速运动,![]()
切割磁感线的有效长度为:![]()
产生感应电动势:![]()
![]()
回路的瞬时电阻:![]()
功率:![]()
金属棒运动到D点,所需的时间设为![]() ,则有:
,则有: ![]()
解得:![]()
当![]() 时,
时, ![]()

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目